Is Chomskys universal grammar synthetic a priori?

Question

Chomskys notion of a universal grammar is his way of comprehending that human languages appear to have a deep grammar, and that children appear to learn language as though they are primed for it.

It was Kant that isolated the question of whether synthetic a priori knowledge is possible, and he suggested that this question hadn't been asked before; he suggested that this was possible, and placed under this rubric mathematics and our understanding of space & time.

Now, does language fall under this? Certainly, it appears that each specific & particular language cannot be, as they are contingent on how language has developed in the social world a hman being is born into. But can one say the same about Chomskys notion of universal grammar, which he claimed is innate?

Answer 1

Innate does not imply a priori. Suppose we humans are so configured as to be innately afraid of heights (or, as ducklings, to strongly attach to the first person we see). And suppose this manifests to us as beliefs, so that all humans believe innately that heights are dangerous and mothers are wonderful. It should be clear that neither of these beliefs count as a priori simply because of their innateness, despite needing no personal experience to come to believe them.

Universal grammar, if it exists, would be an innate feature of humans. But it wouldn't be an innate feature of all possible rational creatures (whereas logic presumably would). Sufficiently advanced space aliens wouldn't necessarily share that "universal grammar". Therefore, it isn't a priori.

Answer 2

There is a difference between "ability" and "synthetic knowledge." For example, there is no recorded instance of a human being running 100m in less than 9 seconds. That doesn't imply that "all human beings have a synthetic a priori knowledge of sports biomechanics."

Similarly there is an empirical discovery that human short term memory is capable of holding seven (plus or minus two) "chunks" of information. The knowledge that the limit exists, and that the limit is between five and nine chunks, is synthetic knowledge. The limit itself is just a limitation of human brains (an ability to remember more than four chunks and an inability to remember more than nine chunks).

Chomsky's universal grammar is an empirical statement about the biophysical limits of the machinery that human beings seem to use to process language. Most humans seem to have the ability to differentiate between grammatical and ungrammatical sentences in their native language, with a complexity that is approximately equal to the mathematical class of context-free languages. This tells us something about the complexity of the machinery in the human brain that is required to process language. It needs to have more state storage than a finite automaton, approximately the storage ability of a push-down automaton, and probably less state storage than a Turing machine. (That's just determination of gramaticalness, not meaning/understanding.)

Other commonalities between the grammars of human languages is that they all seem to have the same kinds of classes: "nouns", "verbs", "adjectives", and usually have conjugation of verbs and/or declension of nouns and adjectives based on grammatical categories. The grammars and contents of the classes are different in every language, but there is significant structure that all languages share. This, again, tells us something about the complexity and storage capacity of the human machinery that processes language. The fact that there are commonalities in the structure of English, Mandarin, Urdu and Arabic does not mean that we are all born with synthetic a priori knowledge of what that structure is.

Answer 3

I think this is a challenging question, but one that can be thought through in a detailed way. The conclusion I'm going to defend is that a universal grammar that looks anything like what Chomskyans expect will be analytic a priori knowledge -- assuming those terms are indeed well-defined. I'll do my best to select fairly robust definitions of those terms, but keep in mind that anyone who rejects the existence of a priori knowledge, or who rejects the analytic-synthetic distinction, will reject my conclusion as meaningless or ill-formed.

I'll also discuss the lingering possibility that knowledge of a universal grammar might indeed be synthetic a priori knowledge, and what one would have to demonstrate to persuade me of that claim.

Space does not permit a full development of the argument I want to make, so take what I'm offering here only as a rough sketch -- in two parts. I'll begin by talking about aprioricity; then I'll talk about analyticity.

Knowledge of Universal Grammar is A Priori

First, I want to defend the position that if anything is a priori knowledge, then any well-formed universal grammar is a priori knowledge -- regardless of whether it is "innate." The argument is very simple and goes like this:

1. If a priori knowledge exists at all, then any knowledge that we can mathematically formalize is a priori knowledge.
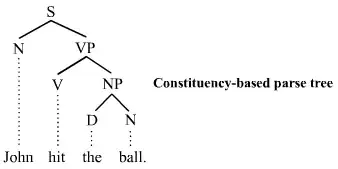
2. A "well-formed universal grammar" is a syntactic structure that we can mathematically formalize.

The desired conclusion immediately follows. Recall that "a priori" knowledge is not necessarily innate knowledge -- it's simply knowledge that can be verified as true without having to turn to experience. (That might always count as "innate" depending on what your definition of "innate" is; but let's not get into that!)

Now, premise one seems indispensable if we're using these terms in ways that are even close to standard. Premise two is defensible because the whole point of Chomskyan grammars is that they can be formalized; for example, transformational grammars can be formalized as tree automata. So if the Chomskyan program is on the right track, then the particular universal grammar inside the heads of all humans is mathematically formalizable, and is therefore a priori knowledge.

Now, what if this grammar isn't really universal? What if different people have different grammars in their heads? I don't think that would change anything. If we have multiple differing grammars inside our heads, they all should still count as a priori knowledge if they are mathematically formalizable. But if there are no mathematically formalizable grammars in our heads, then the Chomskyan program is on the wrong track, and the question stops being coherent. (We would still have a priori knowledge of things like context-free grammars, transformational grammars, pushdown automata, and tree automata! They just wouldn't have any particular relation to the grammars of natural human language.)

Knowledge of Universal Grammar is Analytic

The difficult part of this question is whether our knowledge of a well-formed universal grammar would be synthetic or analytic. Here again, we have to accept that the distinction exists; otherwise the question is incoherent. But what might the distinction mean in this case? In particular, we need a precise understanding of the term "analytic." Then we need to understand what it takes for a priori knowledge to be synthetic. This last problem is very difficult, and I think the best approach is to look at what might make mathematical knowledge synthetic rather than analytic from a post-Fregean point of view.

So I'll begin by turning to Frege's account of analyticity, which is usefully summarized by the SEP. In short, Frege tries to clarify the notion of "containment" that Kant uses to define analyticity. According to Kant, an analytic statement is one that states a fact already contained in the definitions of the terms it uses. So the statement "all bachelors are unmarried" is analytic, but the statement "all bachelors are sad" is synthetic. Frege attempted to refine this definition by linking it to the idea of formal or logical equivalence. If, by a process of purely formal substitution, one can derive a statement from a set of given prior terms, then that statement is analytic.

Now, Frege's hope was that he could show that all arithmetical knowledge was analytic. But there's a convincing argument that he failed. This argument has to do with the problem of the actual existence of mathematical entities. Frege's system explicitly commits itself to the existence of mathematical entities, but the justification for that commitment must be synthetic!

Why should we believe that? Because for any given formalization of arithmetic, there exist diophantine equations that do not have solutions, but that cannot be proven unsolvable within that formalization. Since diophantine equations are really quite elementary components of mathematics, we would like a commitment to the existence of mathematical entities to include a commitment to the existence of diophantine equations. And if we are committed to the existence of those equations, then we would like there to be a fact of the matter whether or not any given diophantine equation is solvable. But if we depend only on analytic knowledge of mathematics -- if we rely only on formalization -- then we have to accept that in some cases, there is not a fact of the matter whether a particular diophantine equation is solvable. The conclusion that there is a fact of the matter is an inescapably synthetic judgment -- it posits the existence of Something outside of the formal system of definitions and substitutions that describes it. But because that Something is strictly mathematical in nature, it seems unreasonable to describe our knowledge of it as a posteriori -- unless you reject the idea of a priori knowledge altogether.

If you don't want to confront this problem, then you don't have to commit yourself to the existence of mathematical entities, but you then give up some kinds of certainty. If you don't want to make that sacrifice, then you have good reason to accept the claim that at least some mathematical knowledge is synthetic a priori knowledge.

So to sum up, it seems we need to say yes to at least three questions to make a convincing claim that some knowledge of X is synthetic a priori knowledge.

1. Is there a truth about X that the formal definition of X doesn't already "contain"?
2. Do we feel a strong motivation to accept that truth rather than remaining agnostic?
3. Is that truth indeed a priori?

Applying these three questions to a hypothetical Chomskyan universal grammar, I think the answer is probably no in all three cases. Now this is where my argument breaks down a bit, because of course there is no established universal grammar yet. It may turn out that linguists discover the actual universal grammar, and find that 1, 2, and 3 are all true of it. But I see no particular reason to accept that conclusion yet!

Furthermore, there as been at least some speculation that universal grammar is itself the very paradigm of analyticity. In this account, it is precisely the structure of the universal grammar that gives us our understanding of analytic truth. In that case, it would seem strange that our knowledge of universal grammar is itself synthetic. On the other hand, there doesn't seem to be a strong reason to assume that it is not. Perhaps the best route is to remain agnostic on the matter. But if I had to place a bet, I'd bet that our knowledge of universal grammar, such as it is, is analytic.

Answer 4

UG (not language as a whole) would be a synthetic a priori, since it is informative (in Kant's sense of synthesis) and it does not depend on experience. Not depending on exprerience should be took with a grain of salt. It obviously doesn't mean independent of each human experience of any human ever been, and it obviously doesn't mean analytic, since that is not what Kant meant by apriority. UG is supposed to be innate in the sense that every human should develop language if exposed to language, but it does not develop on its own and avoiding language exposition to a child will compromise his hability to make use of language, and obviously other problems. The case is that UG is a priori in the sense that UG it is a experience-independent potentiallity common with all humans.

The finite grammar which produces infinite sentences is a inherently synctactic notion. Chomsky in Synctactic Structures makes it clear that he intends to leave semantics as it were in terms of structuralist semantics, by that I mean that his proposal does not involve concepts or meaning as in the meaning of words. UG involves syntax solely.

The guiding process of the whole project is "Given a set of gramatical english sentences, we may now ask ourselves which type of mechanism can produce this set"(CHOMSKY, Synctactic Structures, ch.3, §1). This production of a sentence is given through the series of synctactical rules in which it is possible to derive a gramatical english sentence.

Language is socially constructed in terms of the meaning of particular words and some synctactic possibilities. A subsequent model of linguistics claims an internal structure of principles and parameters, where principles are invariable through human language and parameters are local aspects of a given language (for example, synctactic ordering SVO or SOV). So it is innate as an abstract structured syntax that sets possibilities which can be instantiated with particular words to form sentences. Consider the following:

The structure illustrated by the tree is that which is innate possibility within universal grammar. The particular words are learned. In the beginning of the generative linguistics, the form of derivation of sentences was analogous to that of a derivation in an axiomatic system. The rule of inference from one to another was called the rewriting rule.

The tree above could be constructed by the following rules and a set of words. In syntax, we would have the rules (R1) "S → Nominal Phrase + Verb phrase", (R2) "Verb phrase → Verb + Nominal Phrase" and (R3) "Nominal phrase → determinant + Name". Given a sentence S, we may apply R1, then R2 in the Verb phrase, then R3 in the nominal phrase in the verb phrase. That would give us the tree above illustrated.

Given the terminal nodes in the trees, like V,N or D, we may have a set of words for the chosing, such as V = {hit}, N = {John, Ball} and D={the}. We may then form the phrase "John hit the ball" and "Ball hit the John". The second case may sound strange, but at a synctactical level they are the same.

An observation: synctactic strucutres do heavily influence meaning given the composition of the components of a sentence. It is worthwhile noting the case in which quantifiers are ambiguous relative to the scope of different synctactic structures, e.g. "Every man loves a woman".

Other obs: Language is commonly understood to be organized T-scheme (not Tarski's truth conception) in linguistics.

Deep and shallow structures are synctactic, while the phonetic form has to do with the sounds the language uses, and the logical form deals heavily with quantifier ambiguity with very general semantic structures (not words).

Obs 3: A priori should be considered in Kant's context, so I disagree with an answer about considering a distinction between innateness and apriority. Clearly there is a distinction between a priori and analiticity for Kant, since synthetic a priori does not imply synthetic analytic. a priori in this context should be understood as independent of experience.