0

As far i understand existential import Aristotelian point of view universal statements should talk about things that are exist , But Boolean point of view say that we can talk about any thing . OK ?
But from both standpoints the word some implies existence .
so how they Treat the statement "some unicorns are red"
and why Boole make different standpoint of view in universal statements and keep particular the same as Aristotle ?
and by Boolean standpoint
All s are p = No member of s are outside p .
No s are p = No member of s are inside p .
and Venn diagrams will look like this
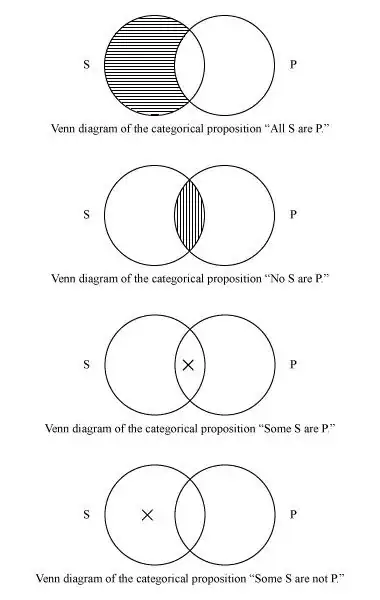
Venn diagrams
But How they will look like in Aristotelian point of view ?

then by existential import they make modern square of opposition
and only relation is contradictory i can understand why sub-alternation is
removed but i can't understand why another relation removed (sub-contrary ,
contrary )?

Abdelrhman Fawzy
  • 257
  • 4
  • 11
  • 1
    Not clear.. See [The Traditional Square of Opposition](https://plato.stanford.edu/entries/square/) and [Existential Import](https://www.jstor.org/stable/40104343?seq=1#page_scan_tab_contents). – Mauro ALLEGRANZA Aug 28 '17 at 08:24
  • See also [In modern logic, why does “All S is P” contradict “Some S is not P”?](https://philosophy.stackexchange.com/questions/33372/in-modern-logic-why-does-all-s-is-p-contradict-some-s-is-not-p) – Mauro ALLEGRANZA Aug 28 '17 at 08:26
  • my questions is 1-sub-contrary and contrary relations removed from modern square? 2- how will Venn diagrams will look in Aristotle viewpoint? 3- why Boole make this view from universal statements only ? – Abdelrhman Fawzy Aug 28 '17 at 08:49
  • 1
    1) because not very useful: *contraries* is the relation between "Every S is P" and "No S is P". The two are not contradictory nor in a relation of logical consequence. – Mauro ALLEGRANZA Aug 28 '17 at 09:37
  • 1
    For Venn diagram for syllogism, see e.g. Patrick Hurley, [A Concise Introduction to Logic](https://books.google.it/books?id=Ikp2dGWT5O4C&printsec=frontcover&dq=Patrick+Hurley+A+Concise+Introduction+to+Logic&hl=it&sa=X&ved=0ahUKEwiF3MnO8PnVAhXCfFAKHdc5DSUQ6AEILzAB#v=onepage&q=Aristotelian%20Standpoint&f=false), Wadsworth (11th ed 2012), page 266 and page 274. – Mauro ALLEGRANZA Aug 28 '17 at 12:02

1 Answers1

3

This convention has to do with Boole's insight that representing True as 1 and False as zero, you can see and as a form of multiplication and or as a form of addition (in binary discarding the carry).

This is quite apt, as 1 * 1 is the only combination that comes out 1, and 0 + 0 is the only combination that comes out 0, the same way True and True is the only combination that gives True, and False or False is the only combination that gives False.

It makes the math work out better if the default value for multiplication is 1, meaning that the product of zero things is 1 by default. That way the product of n things is always the n-th one times the product of its predecessors, even when there aren't any predecessors. This simplifies various common proofs by induction and remove special cases from many famous theorems. The result is so convenient that it is the convention throughout math, including in Boole's artificial interpretation of conjunction as multiplication.

Then, to make universal quantification look just like infinite products of zeros and ones, it works out best if "Is this true of all zero of these things" is answered True, the equivalent of 1 and not with the more obvious False. It doesn't, in fact, matter, because if you wanted to act on this fact, it would tell you something only about nothing. And discussions of the properties of nothing are already conflict-ridden jokes.

The sum of zero things is already more obviously zero.

"Some unicorns are red" means the same thing for both the classical and Boolean cases. It implies there is a red unicorn. The two agree here, because 'Some' is an extension of 'or' and not 'and'. Something is true of some things if it is true of one or another of them.