11

In 12TET, concert G is always at a particular pitch, frequency, etc. However, on instruments such as violin, players will stray slightly to make a note sound more in tune, dependent on key. (As in using a subtly different temperament).

Does that mean that, for instance, G, in key G, will be in one place, but in key Eb, where G is M3, it'll be slightly different, and in Ab, where it's the leading note, it'll be different again? Does it mean that there is a possibility of seven different places where G lives?

Tim
  • 183,051
  • 16
  • 181
  • 444

2 Answers2

16

Yes, if not far more than 7 when you consider pitches outside of the diatonic scale and variations on A440!

By "stray slightly to make a note sound more in tune," you're talking about just intonation.

In 12-tone equal temperament, in C major, let's say C is our "zero-point." For the ensuing discussion, all pitches are based off of this 12TET where C is "0 cents"; the G above it will be 700 cents higher.

In 12TET, this perfect-fifth G is a little low by about 2 cents. So the justly tuned G will actually be around 702 cents.

(As an aside, note that intervallic inversions reverse the difference. Whereas a justly tuned perfect fifth is 2 cents higher than 12TET, the justly tuned perfect fourth is 2 cents lower.)

But now, switching to E-flat major (tonic is now 300 cents), G is our major third. In 12TET, the major third (400 cents higher than tonic) is actually about 14 cents sharp; our justly tuned G is actually at about 686 cents.

But it gets stranger! We're in E minor (tonic is 400 cents), and G is the minor third. In 12TET, that's 300 cents higher than tonic, but it's about 16 cents lower than the justly tuned minor third, which would be tuned at 716 cents.

Especially interesting is that our G, when it's the justly tuned major third, is actually about 30 cents lower than that G when it's a justly tuned minor third, a difference of over a quarter of a tone! (This assumes the two tonic pitches of E and E♭ are exactly 100 cents apart.)

The following table I found seems accurate, though I haven't yet verified everything:

enter image description here

Richard
  • 82,618
  • 16
  • 186
  • 360
  • So 'perfect' is a misnomer. Should be 'nearly perfect', as in 4ths and 5ths. But still closer to perfect than the others! On something like a violin (or even a violin) by the time vibrato is added, that's really going to mess things up. – Tim Apr 19 '18 at 14:54
  • 7
    @Tim My understanding is that vibrato actually cleans things up because it allows the ear to interpret the pitch more favorably than a fixed fundamental frequency would. Since pitch is a perception, we can take advantage of auditory illusions to play with that perception. This is one reason why vibrato is pleasing - it's like dithering. It adds what we might call a fixed amount of "desirable error" to cover up a variable amount of "undesirable error". – Todd Wilcox Apr 19 '18 at 16:43
  • 3
    @ToddWilcox - that may well be true of some instrumental music, but it really grates on my ears when opera singers use it instead of proper vocal vibrato. Sometimes not even sure as to which note they're trying to pitch. – Tim Apr 19 '18 at 17:08
  • 1
    @ToddWilcox- you could look at vibrato that way. Or you could look at it as a way of dirtying up intervals so that your ear hears the right pitch in there somewhere. Both viewpoints work. – Scott Wallace Apr 19 '18 at 17:59
  • @Richard- Your table seems pretty accurate, except for the seventh- I would say that the just intonation seventh is the ratio of 4/7, not 9/16. – Scott Wallace Apr 19 '18 at 18:05
  • @Tim I feel similarly. I think the "spread" of the vibrato makes a difference. – xdhmoore Apr 20 '18 at 00:33
  • 1
    String instrumentalist here: use of vibrato to hide errors is highly looked down upon! Use of vibrato to keep a long note from being boring is 'normal,' as is its use for stylistic effect. Then again, there's the rumor that heavy vibrato only came into style in the earliest days of sound recording, when the equipment would "fade" on a continuous pitch. – Carl Witthoft Apr 20 '18 at 12:26
  • 1
    @ScottWallace I would say the 7th should be 9/5 (a minor third above the fifth). Most just intonation is 5-limit, which ignores prime factors greater than 5. The harmonic seventh is over 31 cents low compared to the equal tempered one, and the difference between it and the just minor third above the just fifth is nearly 49 cents--almost a quarter step. On the other hand, if you want your minor seventh to serve as the root of a triad whose fifth is the fourth, then it has to be 16/9 rather than 9/5, and certainly not 7/4, which would give fifth of 729 cents. Just intonation is fluid, not fixed. – phoog Feb 04 '19 at 21:55
  • 1
    @phoog - it's a matter of taste and definition. For me, just intonation means intervals taken from the harmonic sequence of one fundamental tone. That eliminates 9/5, because it's not in the harmonic sequence of 1. And I don't want my seventh to serve as a root- it should serve as a seventh to 1, which it does, more consonantly than 9/5. But as I say, it's a matter of definition and taste. – Scott Wallace Feb 06 '19 at 15:17
3

Does that mean that, for instance, G, in key G, will be in one place, but in key Eb, where G is M3, it'll be slightly different, and in Ab, where it's the leading note, it'll be different again? Does it mean that there is a possibility of seven different places where G lives?

No, it's worse than that. The location of any note can change in a single key, in a single piece, and in a single phrase. That is, it's not so much according to the key of a piece as it is according to the harmonic context of each note. Consider that G in the context of a piece in A minor. The G could be the fifth of a C-major chord. If you get to the C by way of an F chord, and you want the major third between the F and the A to be pure, the ratio between A and C will be 6/5:

A = 440 Hz
C = A * 6/5 = 528 Hz
G = C * 3/2 = 792 Hz

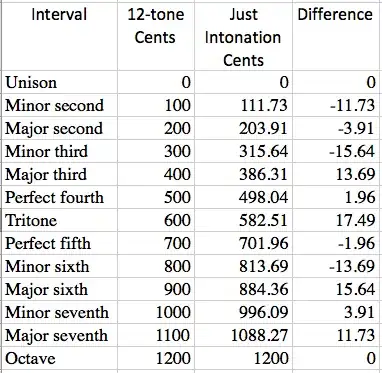
The ratio of G to A is therefore 9/5, which is about 17.6 cents higher than an equal-tempered G at 784.0 Hz.

Now G could also be a fourth above D or, equivalently, a fifth below it. Going from A to G on the circle of fifths, you get a ratio of 16/9:

A = 440.0 Hz
D = A * 4/3 = 586.7 Hz
G = D * 4/3 = 782.2 Hz

That is pretty close to an equal-tempered G, being about 3.9 cents lower. The ratio of the two Gs, 81/80, or about 21.5 cents, is known as the syntonic comma.

So, when you're playing in A minor, and there's a section of the piece where the harmony is focused on D, you might use a different G from the one in another section of the same piece where the harmony is focused on F and C.

You can even find situations where it makes sense to change the pitch of a repeated note because of the harmonic context. This happens, for example, in the final chorale of Cantata 78, Jesu, der du meine Seele. The piece is in G minor, so we'll try to keep G constant. The first pitch where we'll notice trouble is A.

The first four measures are fairly stable and end on the dominant, D major. The next four measures essentialy repeat this, and measure 10 also starts on D major:

X:1
L:1/8
M:4/4
K:Gm
%%score S A T B
V:S            clef=treble name="S"
V:A            clef=treble name="A"
V:T            clef=treble name="T"
V:B            clef=bass   name="B"
% 1
[V:S]  A2   B2   c2   A2   | B2   AG   G2   F2   |
[V:A] ^F2   G2   G2   F2   | F2   F2  =E2   C2   |
[V:T]  d2   d2   c2   c2   | Bc   d2   cB   A2   |
[V:B]  D,2  G,F, =E,2 F,2  | D,2  B,,2 C,2  F,2  |

In analyzing the frequencies, we'll give everything as the ratio with the frequency of G, keeping all the ratios between 1 and 2 by multiplying by a power of 2 where necessary (for example, if we calculate a frequency of 40/9, we'll divide by 4 to get 10/9).

Calculating the frequencies for F# and A from D=3/2, we get F#=15/8 and A=9/8. The tenor carries the D from the first beat to the second, giving us a standard G minor chord of G=1/1, Bb=6/5, and D=3/2. The alto carries the G into the third beat, giving us C=4/3 and E=5/3. The tenor carries the C into the fourth beat, giving F=16/9 and A=10/9.

Here we have our first problem. The soprano just started the phrase singing A=9/8, and now they're singing A=10/9. The ratio of those frequencies is 81/80, the syntonic comma. In fact, if we keep all of the fifths and unisons perfectly in tune, the pitch of the final chord will be lower than that of the starting chord by this ratio. A progression like this is called a comma pump.

How can we fix that? Since the soprano melody is the starting point of the composition, what happens if we tune that chord to the sopranos singing A=9/8 to match their first note, instead of tuning it to the tenors? The bass and alto F becomes F=9/5 instead of F=16/9. Perhaps most oddly, the tenors would have to raise the pitch of the repeated C from C=4/3 to C=27/20. The basses would have to sing a very large half step of 27/25 (33 cents larger than an equal-tempered half step, and 21 cents larger than the usual just half step of 16/15, which is already somewhat large at 112 cents). But when we get to the end of the piece, we'll be back where we started.

But there's still a problem. We're giving priority to the sopranos, and they have an odd interval between their A=9/8 and their C=4/3. That's a minor third of 32/27 instead of 6/5. But hey! If we put the C in beat 3 at C=27/20, the tenors don't have to change the pitch of the repeated C between beats 3 and 4. This could be good. What implications does it have?

If the C of beat 3 is C=27/20, then the G must be G=81/80. Perhaps we can forgive an unstable G in this part of the piece, since we're moving to the relative major. But if we use that G in the previous beat, the D would also have to be raised by a syntonic comma, so either the tenors would have to alter the pitch of their repeated D between beats 1 and 2 or the altos would have to raise the pitch of their repeated D between beats 2 and 3. There's no way to keep all the harmonic and melodic intervals pure while also ending the piece where we started.

phoog
  • 16,807
  • 2
  • 33
  • 61