7

Is there a change in the universe that cannot be reduced to movement? One counter-example should be enough. :)

Heat is a type of change that was once thought to be qualitative, but is now realized to be quantitative, the movement of particles. So perhaps that's true for all change, then?

Excluding the hypothetical change from non-existence to existence of the universe (assuming time has a beginning).

Entanglement might be one example of change without movement? But someone would have to confirm. Wave function collapse perhaps another.

J D
  • 19,541
  • 3
  • 18
  • 83
Olle Härstedt
  • 179
  • 4
  • 2
    This question was closed on Physics: [Is all change movement?](https://physics.stackexchange.com/questions/767795/is-all-change-movement) – Olle Härstedt Jun 11 '23 at 11:40
  • If time can exist in a vaccuum, does time change without movement? Outside of a vaccuum, can time be reduced to movement? – Futilitarian Jun 11 '23 at 12:38
  • @OlleHärstedt Creation and annihilation of particle-antiparticle pair is also a change without movement. – Agnibho Dutta Jun 11 '23 at 13:59
  • 1
    Sebastian Riese gave you a good answer on the physics stackexchange: motion is not a fundamental concept the way physics is done now. Is a changing EM field or wavefunction "moving"? – causative Jun 11 '23 at 14:13
  • 1
    Physics doesn't care much about what non-predictive words are used to describe a phenomenon. If you can rephrase this so that it's a question about what somebody would measure, it'll be more answerable from a physics perspective. – g s Jun 11 '23 at 14:57
  • 1
    [Electron–positron annihilation](https://en.wikipedia.org/wiki/Electron%E2%80%93positron_annihilation) with photons emitted. All three are elementary particles, as far as we know, so there is nothing to move around in electrons and positrons to produce photons as the output (as it happens in chemical reactions). The change is "purely qualitative". Other transmutations of elementary particles have the same character. Entanglement is a state, not a change. Wave function collapse would work if it were real, but it is often interpreted as mere reconditioning of probabilities. – Conifold Jun 11 '23 at 20:39
  • Thanks @Conifold :) Do you know if string theory would make this change quantitative instead of qualitative? Speculation from my side, I know nothing about string theory actually. – Olle Härstedt Jun 11 '23 at 20:46
  • 2
    Maybe, elementary particles are supposed to be vibrating strings, but it introduces transmutations of its own. The mechanistic idea of "particles in motion" doing all the change died with mechanical models of aether, and was buried along with the concept of classical particles by quantum theory. String theory is an extension of quantum mechanics, not of classical one. There are no more immutable elements recombining, all proposed 'elements' transmute into energy and each other. – Conifold Jun 11 '23 at 21:06
  • 1
    What do you mean by movement? A change of location in space? Is a change of location in spacetime movement? Or is anything you call 'movement' movement? –  Jun 12 '23 at 14:44
  • The question can be reversed, and ask is there any example of a change that *didn't* involve something moving in space? I would argue that no such change exists, and that in fact the so-called "time dimension" is merely derived in a complicated way from the 3 spatial dimensions alone. – Steve Jun 12 '23 at 16:24
  • *"died with mechanical models of aether"* - I think you'll find it didn't die, it's a fully live interpretation that is merely neglected by a scholastic physics profession. – Steve Jun 12 '23 at 16:30
  • 1
    Because this is philosophy, I just want to note that absent a purely materialist view, mental changes do not necessarily require movement (one might say that the mental change results in movement or is caused by movement, depending on one's view of the brain). – Spitemaster Jun 13 '23 at 14:54
  • Can you first say how 'Heat…' any more than 'depth, height or width, age or weight or wavelength' is 'a type of change'? 'Heating' is a type of change, but how is 'heating' the same as 'heat' any more than 'movement' is the same as 'position'… in mechanics or here in Philosophy? – Robbie Goodwin Jun 25 '23 at 20:36

8 Answers8

7

Annihilation and creation of particle-antiparticle pair is also an example of change without movement.

Wavefunction collapse and entanglement are also changes without movement if you do not consider information exchange as movement. In these processes, information exchange takes place.ㅤㅤㅤㅤㅤㅤㅤㅤ

However, if it comes down to the school of philosophy you follow. If consider information exchange as "movement" then, wave collapse and entanglement are changes that involve movement.

Warning:-

Here, by the word "movement", I mean movement through only the spatial direction. Everything in this universe is moving through one or more dimensions of 4D spacetime.

Moreover, an object may seem to be in a form of movement in your reference frame but in other refrence frames it may be stationary. Actually, concept of "movement" is not well defined in physics as it is not Lorentz invariant.

Agnibho Dutta
  • 459
  • 1
  • 15
  • Easier still, one particle decaying into simpler particles cannot be reduced to movement alone. – Daron Jun 12 '23 at 08:02
  • 2
    This answer appears to have been [cross-posted with the question](https://physics.stackexchange.com/a/767913/44126). – rob Jun 12 '23 at 09:58
6

If you believe so, you are making the claim in the same spirit Hobbes did. Hobbes said:

"all change is motion"

The argument goes like this:

  • All time is defined in term of motion. A day is a rotation of the earth, a year an ellipse about the sun, a second is a merely a fraction of the day.
  • All change occurs over time.
  • Thus, change by way of time requires motion.
J D
  • 19,541
  • 3
  • 18
  • 83
  • Upvoted for simplicity and clarity, but it's worth noting that this setup is not especially physical. One could argue that [proper time](https://en.wikipedia.org/wiki/Proper_time) is defined in terms of motion, but lightcone time is defined in terms of distance (space-like separations). – Corbin Jun 13 '23 at 16:03
  • 1
    @Corbin It is indeed. Hobbes grasp of relativistic physics is clearly lacking. :D It's fair to caution the OP that the thinking of Hobbes might be considered historical metaphysics and somewhat indefensible under the ideas of modern physics. – J D Jun 13 '23 at 20:35
4

It's a bit of a word-tangling question. Because, how would you know change was happing within a subsystem, without messing with it and so changing it?

I recommend the Quanta Magazine article on the topic: Is Perpetual Motion Possible at the Quantum Level?

It is interesting to consider visible-scale quantum objects, like described in this TED Talk. However, note they must still be highly isolated as a subsystem to display this behaviour, regardless of scale. Information about Schrodingers Cat would leak out of that subsytem in all kinds of ways, plus is could be considered as an assembly of systems not in quantum coherence anyway, and so oberving each other.

Entanglement doesn't have to imply change. It's like you spin a coin, cut in half while it's still spinning, & no one knows which half is heads or tails until you check one, and that will determine the other - but arguably it will have always been that opposite answer, not change into it by a signal, nor be determined by local hidden variables. See that case put entertainingly here: SMBC 'The Talk'.

However, there is a 2013 conjecture by Susskind and Malcadena, that EPR (entanglement) = ER (Einstein-Rosen Bridges, sometimes dubbed 'wormholes' but subtly different). They built on this to suggest space-time geometry is determined by entanglement. That is certainly interesting, and proposed and developed byvsome of the most significant modern physicists, but, it's just one approach in a crowded field attempting to reconcile QFT and GR. It sits uncomfortably as a proposal with the apparent linearity of unentangled particles, leaving us no apparent way to tell without a record of the entanglement happening, if a state is entangled.

If ER = EPR is true, then information will pass through the bridge. But just as entanglement can't be used to send signals faster than light, it must be noted it can't be quite like how we imagine a wormhole, as connecting distant points like a tube for anything to pass through.

CriglCragl
  • 19,444
  • 4
  • 23
  • 65
3

Physical Laws

I think there is a sentence or paragraph embedded in my old Physics textbook from early 1980s, by Haliday and Resnick, that expresses the following main ideas. I am paraphrasing from memory. During a natural process there are some physical quantities that change and other physical quantities that remain the same. We use the constant physical quantities to solve for changes in the other physical quantities when given sufficient initial information to complete the solution.

The more things change in physics, the more they remain the same!

Galileo

https://faculty.wcas.northwestern.edu/infocom/Ideas/galileo.html

Galileo realized that no one really understood motion at all ...

enter image description here

Galileo discover truths about motion that had completely eluded everyone since the time of Eudoxus, over 2000 years before. Among his discoveries:

  1. In the absence of air friction, all things fall at exactly the same acceleration, regardless of mass, size, shape, or composition.

  2. In the absence of friction, anything set into linear motion will stay in motion forever.

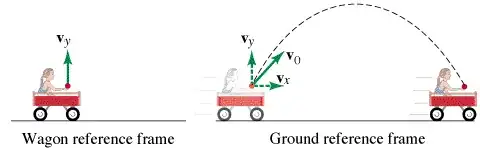
  3. If one combines the two principles above, then it must be true that an object dropped from a moving platform (or tossed in the air) does not fall directly towards the Earth, but in fact moves along a curved path such that it remains abreast of the (still moving) platform.

From the viewpoint of a person on a moving wagon, a ball tossed in the air goes straight up. But from the viewpoint of a person on the ground, the ball moves in an arc such that it always remains above the moving wagon. These laws constitute the basis of what is today called Galilean Relativity. They explained how it was that the Earth could move without anything "pushing" it -- in so many words, Aristotle had it exactly backwards. Once in motion, the Earth (or anything else) will continue to move forever unless some force intervenes to stop it. Friction stops everyday objects, but there is nothing to stop a planet in its orbit. Furthermore, once an object acquires a velocity, it keeps it. A ball dropped from the Leaning Tower of Pisa already shares any velocity that the Tower has as the Earth rotates. As the ball drops, the Tower, the Earth, and the ball all move together. Their "absolute" motion cannot be measured. Only the ball's relative motion with respect to the Earth and the Tower can ever be detected.

Or to phrase it another way, to say that something is "moving" is almost meaningless. You can only say that something is moving with respect to something else. This is the essence of Galilean Relativity. One way of thinking about relativity is this: if you are placed inside a closed box, with no way of detecting anything outside the box, then there is NO experiment you can do inside the box, NO measurement you can possibly make, which will tell you if you are moving (at a constant velocity) with respect to anything outside the box or not. Everything inside the box shares your velocity, and measurements on those can only tell you how you are moving with respect to them -- not how they (and you) are moving with respect to something else. This is very different from the physics of Aristotle, who held that objects had an absolute tendency to move straight towards the center of Earth, no matter what the circumstances.

Galileo defines speed as change in position (displacement) specified with respect to a reference frame divided by the change in time specified with respect to a clock. He describes acceleration as the change in speed divided by the change in time. Galileo took discrete measurements. We could put his specified discrete values into difference tables to understand or teach his math models.

Newton "stands on the shoulders of giants", such as Kepler and Galileo, and defines momentum as the mass of a body times its velocity with respect to an imposed frame of reference. He defines force, the tendency to change momentum, as mass times acceleration for a "free body" where this means net force causes acceleration with respect to an arbitrarily imposed non-accelerated frame of reference. If forces are in equilibrium then the net force is zero and the body does not change momentum.

Specified momentum has no absolute "true value" because a change in reference frame or change in standard mass units of measure will give a different specified value. Velocity is displacement (change in position in space) over a period of time. This is motion or no motion in the frame of reference. There is a scientific theory which holds that momentum is conserved on the macroscopic and microscopic levels for particle interactions. This is implied in Newton's third law: for every action (force) there is an equal and opposite reaction (the reactive force).

As I understand the math models and solutions, the main idea is that all physical changes involve efforts to measure changes in momentum over time in a region or regions of space whether on a macroscopic or microscopic level. An electron transition in an atom in the Sun emits EM radiation via the loss of quantum energy, and then later, an atom in the earth or some other distant body absorbs the same amount of quantum energy. Electromagnetic waves are emitted and detected as changes in momentum and energy states of microscopic particles in the context of action at a distance. Gravity is a macroscopic change in momentum in the context of action at a distance. Macroscopic friction and loss of mechanical or electrical or magnetic energy are accounted for by the the transfer of heat at a microscopic level that tends to transfer thermal energy from a system to its surroundings. This model does not violate the principles of conservation of momentum or energy because heat, work, and energy are equivalent.

If we did not have the concept of macroscopic motion, I do not think we would have developed the concepts of thermodynamics, quantum energy state transitions, and action at a distance due to radiation or even entanglement, although there is only abstract math in modern quantum theory.

SystemTheory
  • 614
  • 3
  • 6
1

Time itself if simplified can in some ways be considered as changing without motion, trivially, so that's a kind of conceptual change that is not reducible to motion (but this view can be challenged in various ways).

This allows for other abstract changes like "identity" or "property". Such as your legal ownership of a house may contractually end at a certain date.

Space itself could logically change shape (e.g. expand) without any object in that space changing their positions to each other as defined by space, but I don't know if that's a physical possibility that can happen without motion.

Other than that, some change that involves motion may not be reduced to motion, if instead it can be reduced to forces like gravity or magnetism.

Outside physicalism, other things might change without motion, as an example the love between two persons can change without physical change if one believes in a form of dualism where love is located entirely outside the physical without physical correlate.

Also in theoretical worlds that are not our universe, we can conceive of changes that would happen without involving motion, such as objects changing color in a fantasy universe where color is a non-reducible property of atoms.

The latter is an example for logical changes that are not reducable motion (only): Emergence (creation), Fusion, Fission, Transformation, Annihilation.

There are also changes that are for practical reasons difficult to reduce to motion, such as how the English language evolved over time, or how a human improves their skill at playing chess, though arguably they remove reducable to motions in principle.

tkruse
  • 3,397
  • 6
  • 21
  • 1
    Time usually has an operational definition of "what the clock shows" (where clock can be as simple as the thing on the wall and as complex as measuring the change in hyper fine structures of particular atoms). So either way our measurement of time at least very much rests on the "a given action in a given system takes a set amount of time", but if we for example due to effects of special relativity experience our world slower as usual so does our perception of time change. So it's usually space-time where it's yet again movement. – haxor789 Jun 12 '23 at 06:49
  • 2
    I agree that the first version of my answer invites such arguments. – tkruse Jun 12 '23 at 07:32
1

Epistemologically, we exist in two dimensions: physical (what is perceived by the senses) and metaphysical (what occurs in the mind, independently of the senses).

You refer to physical change. But change is also metaphysical, which is a huge domain.

If a belief that changes (e.g. today I love, tomorrow I don't) can be reduced to a physical change, it will be physical. But for now, nobody has proven that metaphysical facts can be reduced to physics (see about the hard problem of consciousness).

RodolfoAP
  • 6,580
  • 12
  • 29
  • 1
    *"metaphysical (what occurs in the mind, independently of the senses)"* Pretty contentious. The Cogito picture of a free-floating-brain can't be reconciled with the Private Language Argument, nevermind with physicalist-materialism/science – CriglCragl Jun 12 '23 at 17:39
1

No. All changes require movement.

There is nothing that change without application of force and force by definition is something that causes motion.

So, excluding creation from nothing (first creation, as opposed to rearrangement/transformation) which you have excluded in your question, there is no change without some kind of motion.

Creation of an elementary particle that we observe is transformation of energy into particle. It requires some kind of contact. That contact only come when there is a movement of some other particle or energy to the site. Annhiliation works in same way. A particle and its anti particle move and only by that movement come in contact with each other. The annhiliation is just conversion of mass into energy.

If a particle fall into black hole and thus get annhiliated then well it has to fall in the black hole i.e. move (or the blackhole has to move to the particle). Also, its still just a transformation. Mass of black hole increase for example.

An elementary particle "sitting" idly in an otherwise empty portion of universe with no net force acting on it do not spontaneously change into something else, do not cease to exist and no property of it change in anyway. For this thought experiment consider forces balancing each other.

Particles that decay decay spontaneously but they are always composite particles (such as nucleus of a heavy atom). There already are forces inside acting on the constituents. Being forces they cause motion and particular types of motions break the particle apart - which we call decay.

seek_knowledge
  • 27
  • 3
  • 3
    This is very informative, thank you. The use of definition of force nailed it. – inform_me Jun 12 '23 at 15:11
  • 2
    Three-body dynamics are an example if how an initially stable system, can have complex nonlinear changes, without applying any external force. Perturbative contributions of things like a photon temporarily turning into an electron-posiyron flight, have real consequences for interactions, so don't we have to picture them as 'part of how photons are' even in the absence of interactions..? They can be related to photon polarisation, for instance. Things entering an event horizon aren't *necessarily* destroyed, we just can't get information back. Eg It's thought a superfluid core may form inside. – CriglCragl Jun 12 '23 at 17:33
  • I'd think a quantum state change of parameters not related to the position in the standard 3D space might be assumed to be not a movement. Even when quantum theories consider extra dimensions, whether that's actually a position in space or just a comfy way to describe something not positioned in the space is a metaphysical question. – rus9384 Jun 12 '23 at 18:25
  • 1
    Hm maybe my question wasn't fully clear, but "change requiring movement" is not the same as "all change being possible to reduce to movement". Right? – Olle Härstedt Jun 12 '23 at 19:18
  • A muon decays in an electron and neutrinos but is not composite. – pygri Jun 13 '23 at 12:14
  • When a muon decay the parts it breaks into moves away. They dont stay where they were before the change. – seek_knowledge Jun 18 '23 at 16:20
0

The Fence Changes along its Length.

enter image description here

Imagine a long fence built near the sea. 10 years ago we painted the fence white. The seaward side has most of the paint stripped off by the salty wind. The landward side is still pristine.

We say "The fence changes towards the sea". But the fence does not move.

Daron
  • 809
  • 4
  • 11
  • Hasn't the lost paint moved, as the wind blew it away? – rob Jun 12 '23 at 09:51
  • 1
    @rob I am referring to the change from one end of the fence to the other. Not the change between the newly painted fence and the current fence. – Daron Jun 12 '23 at 10:22
  • 2
    The question of the OP seems to ask about changes along the dimension of time, not of space (else "motion" makes little sense). This answer is more about linguistics and the fact that "change" can also be applied along a spatial dimension. Else, what "moves" in the answer is the gaze (location of reference) of the observer along the fence, so there is movement after all, just not of the fence. – tkruse Jun 12 '23 at 13:47
  • When you say the fence changes as you move along it, then you are moving as is your mind. Thus, even with change-as-differs, motion is necessary. – J D Jun 12 '23 at 17:07
  • @tkruse The linguistics are important. As is a clear definition. Otherwise you might unknowingly have defined change to involve movement by definition, and hence disguised a metaphysical answer as a tautological one. – Daron Jun 13 '23 at 11:44
  • @JD Yes I move along the fence but the fence does not move. – Daron Jun 13 '23 at 11:44
  • @Daron Not to go physics on you, but there is no privileged reference frame. If you move along the fence, then the fence can be seen in motion relative to you. – J D Jun 13 '23 at 17:08
  • @tkruse Not at all. Motion has multiple senses so, "The fence changes (in quality as we move along it) without changing (in position relative to the earth) resolves the paradox you created nicely." – J D Jun 13 '23 at 17:09
  • @tkruse I don't follow you. – Daron Jun 13 '23 at 18:09
  • @JD Oof, take that Newton! – Daron Jun 13 '23 at 18:10