3

Zeno's paradoxes are paradoxical because they show that in a world of continuous time and space, there cannot be any motion, thus all motion that we see are some kind of illusion. His paradoxes then rely on the infinite divisibility of real numbers which would be identical to chopping up continuous space/time and coming to the conclusion that no task can ever be completed in any finite amount of time. The stadium paradox however shows that the idea of discrete space is problematic too, that discreteness of space which would solve the earlier paradoxes of Achilles and the tortoise, or the arrow paradox, cannot solve the stadium paradox.

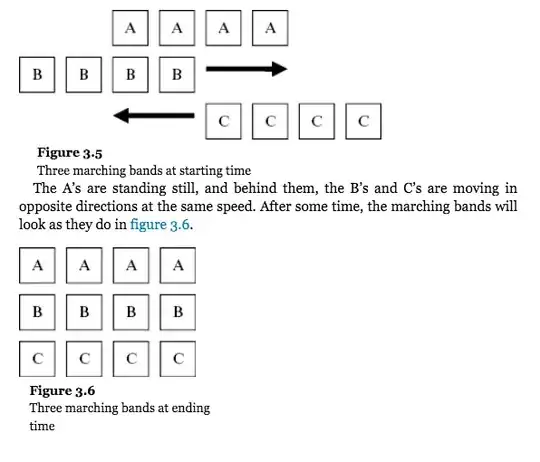
The stadium paradox goes like this: Row A is occupying 3 quanta of space, while row B is moving right at maximum velocity, and row C is moving left at maximum velocity. In the time row B surpasses two quanta of space from A's perspective, row B also passes 4 quanta of space from C's perspective. If there is a discrete absolute space, this paradox is unsolvable. Stadium Paradox

Relativity would solve this problem by contracting space at C from B's perspective and the same with A to a lesser degree. However, you cannot contract discrete space because that contradicts our assumption of discreteness, so space must be continuous in order to allow such a contraction. So to explain the general phenomenon that we observe, we must assume that space and consequently time are both discrete and continuous and the paradox remains.

What should one make out of this? Can this paradox be solved? If not, does it mean that there is no motion or dynamics in the world?

Weezy
  • 389
  • 1
  • 10
  • Comments are not for extended discussion; this conversation has been [moved to chat](https://chat.stackexchange.com/rooms/108820/discussion-on-question-by-weezy-zenos-stadium-paradox-if-space-is-not-continuo). – Geoffrey Thomas Jun 03 '20 at 07:10

4 Answers4

2

The problem will all paradoxes of this particular sort is actually a problem of language: we don't have a good way (in spoken language or specialized languages like mathematics) to conceptualize tensors. The paradoxes work by slicing movement into a series of discrete, static positions separated by instantaneous movements between those positions, as though objects move by standing perfectly still for some epsilon (a small but non-zero period of time) and then jumping to a new position where they again stand perfectly still. The problem reduces to a question of how objects make that instantaneous jump, which (reasonably enough) seems impossible. But all that really shows us is that we don't how to talk about position and movement in the same breath.

Think of Zeno as an early incarnation of the quantum uncertainty principle, if that helps (though somehow I doubt it will...).

Ted Wrigley
  • 17,769
  • 2
  • 20
  • 51
1

It is not a paradox at all

At the time Zeno lived, coordinate systems and frames of reference were not yet being invented and studied. You really do not need relativity to solve this. All you need is to write down speeds in 3 coordinate systems : A, B, C with corresponding reference points. In system A va=0, vb=2, vc=-2 . In system B va=-2, vb=0, vc=-4 . Finally, in system C va =2, vb=4 and vc = 0. You could freely transform speeds from one system to others via relative speed. For example, since in system C vb=4, you need to substract 4 from all speeds in system C to get their values in system B .

As we can see, there is no difference between continual or discrete spaces in this, as long as we can find way to measure speed. Since original "paradox" already defined space (size of rows) and assuming they have equal time units in all 3 systems (which is reasonable considering distances and speeds involved), then they have measurable speeds. However, it is completely correct to take this as one proof that "absolute space" (i.e. absolute frame of reference ) does not exist.

rs.29
  • 1,166
  • 4
  • 9
0

Space is a relation between the viewer and reality. That is actually part of its origin. That is, space is a derived phenomenon, not an innate part of the universe.

Marxos
  • 735
  • 3
  • 12
  • But the viewer is itself a part of reality. Where do you draw the distinction? – Weezy Jun 04 '20 at 20:01
  • The distinction of subject vs. object is quite clear to every human. Why build a problem when there isn't one? – Marxos Jun 04 '20 at 20:04
  • if it is so obvious, what is stopping you from spelling it out explicitly? – Weezy Jun 04 '20 at 20:05
  • You. As the soul is a collective and shared phenomenon, your denial creates part of a reality. – Marxos Jun 04 '20 at 20:06
  • I feel lost. Shared phenomenon being shared with what? I can see the idea of individual souls, but how does that make it shared? And who is denying what? – Weezy Jun 04 '20 at 20:11
  • Space relationalism is debated much later and countered by Newton's famous Bucket Argument... Here Zeno just tried to support Parmenides' doctrine that contrary to the evidence of one's senses, the belief in plurality and change is mistaken (oppose to Heraclitus's views), and in particular that motion (as commonly viewed as plurality over a naive disjunction of extendable spaces) is nothing but a epistemic illusion. Of course Zeno's paradox (argument) seems inaccurate under modern calculus framework as he mistook measuring displacement as counting instants at its root.... – Double Knot Apr 05 '21 at 00:33
  • @Weezy The main reason that ideas of individual souls can be shared is due to ontological categorical features of such an individual soul. We cannot share any linguistic or symbolic concepts with ants, but can communicate effectively to a certain degree (not absolutely perfect though) with fellow sensible common human beings, especially those within a same or similar intellectual community. This is our innate characters and why we're rational a prior, not purely empirical. – Double Knot Apr 05 '21 at 01:17
0

May be here you could find one way of solution this paradox:

Discrete Space and Zeno's Paradoxe 'The Moving Rows or Stadium'

Kristian Berry
  • 9,561
  • 1
  • 12
  • 33
Cherant
  • 1
  • 1
    Hello, and welcome to Philosophy.SE. Would you be so kind and explain *why* you think this paper is relevant, maybe embellished with quotes? As it stands, this post is not a useful answer. – Philip Klöcking Apr 04 '21 at 19:14
  • Hello. First, the conclusion from Achilles and tortoise paradox that time and space could be discrete. Second, the conclusion of Moving arrows paradox is that time and space couldnt be discrete. Becouse if particle A moving to particle B so could be situation when particle A and B must shared the same space and time cell (in discrete space and time world). But if you imagine that in Micro Micro part of discrete space and time world couldnt be the same time when A and B near each other. In simple words A have A time and B have B time (the move of time notion) so you could solve Arrows paradox – Cherant Apr 06 '21 at 03:38
  • Sorry, my previous comment about Stadium paradox of course. – Cherant Apr 06 '21 at 06:23