Without truth tables, how can I deduce that P → Q ≡ ¬P ∨ Q?

Question

From: Philip Johnson-Laird BA PhD Psychology (UCL), Stuart Professor of Psychology Emeritus at Princeton. (Author isn't a logician.) How We Reason (1st edn 2008). p. 108.

I changed the author's choice of first names, to ones that start with P and Q to fit the title.

I symbolized the disjunctions in square brackets. Please don't use truth tables.

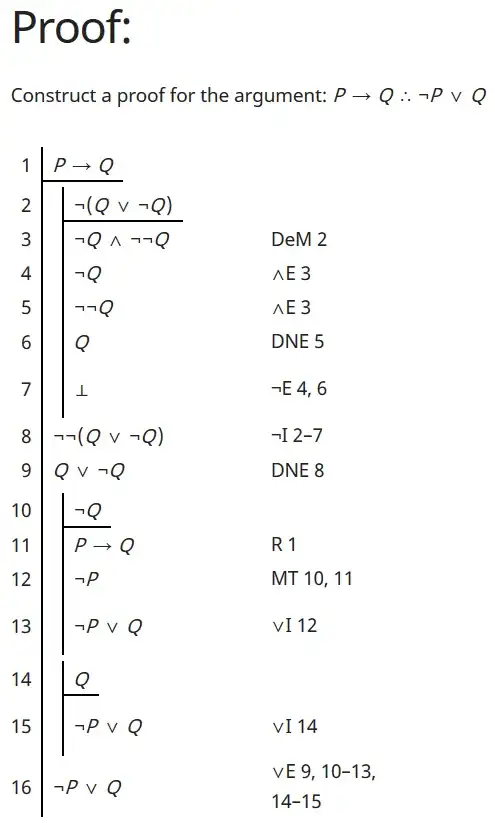
¬P ∨ Q never appears in these quoted sentences. So how can I conclude ¬P ∨ Q from them?

An exclusive disjunction, such as:

Either Pia helped or Quinn helped, but not both

is equivalent to the proposition:

Pia helped or the Quinn helped, and not both Pia helped and the Quinn helped.

Hence, exclusive disjunction also has a logical meaning.
In an analogous way we can define a logical meaning of “if”. The sentence:

If Pia didn’t help then Quinn did. [If ¬P, then Q.]

means:

Pia helped or Quinn did, or both. [P ∨ Q]

In its logical meaning, the conditional is compatible with three possibilities: Pia didn’t help and Quinn did [¬P ∧ Q] , Pia helped and Quinn didn’t [P ∧ ¬Q], Pia helped and Quinn helped [P ∧ Q]. The only possibility that the conditional rules out is that neither the Pia nor Quinn helped [¬P ∧ ¬Q]. The three possibilities that the conditional allows are the same as those for the inclusive disjunction.

p. 478 (footnote for Ch. 21) introduces the psychology:

309. Ormerod and his colleagues show that participants can infer conditionals from disjunctions, and disjunctions from conditionals (see Ormerod et al., 1993, and Richardson and Ormerod, 1997). For example, given the conditional:

If Phil’s next grant application isn’t going to be funded then he’ll be disappointed

we can infer the disjunction:

Phil’s next grant application is going to be funded or he’ll be disappointed

But, the results corroborate a prediction from the model theory: it is easier to make the converse inference from a disjunction to a conditional. They also bear out Ormerod’s claim—now embodied in the model theory—that we prefer to work with as parsimonious models as possible. In unpublished studies, Sonja Geiger has found that participants who carry out this paraphrasing task before they estimate the probability of a conditional tend to take more possibilities into account in their estimates

Answer 1

First, I'll say that the paragraph implicitly uses truth tables to compare the cases where P -> Q and ~P v Q, finding them to be the same.

Any statement that can be proven with a proof table (ie, any statement in sentential logic) can be proven with natural deduction instead. And natural deduction can be extended to prove statements in several other, more-powerful logics. There's a number of ways to formalize natural deduction; I'll use the system in forall x: Calgary Remix because it's freely available online and has an automatic proof checker (which is what I used to write the proof below).

(I learned natural deduction using Teller's A Modern Formal Logic Primer, which I think is superior, but it doesn't have as many modern comforts.)

This might all be a bit hard to understand. I'll give explanation a shot, but unfortunately I don't think there's a good, concise way to explain what's going on; you've just got to learn natural deduction or it won't make sense.

I start with the premise P -> Q and then assume towards contradiction that ~(Q v ~Q). As I'm able to derive a contradiction from that statement, it must be false; therefore I can conclude ~~(Q v ~Q), which is equivalent to Q v ~Q.

If we have A v B, and A -> C and B -> C, then it must be the case that C, because no matter which is true between A and B, C is also true. So the second half of the proof is showing that Q and ~Q, in combination with our premise of P -> Q, both imply ~P v Q. QED.