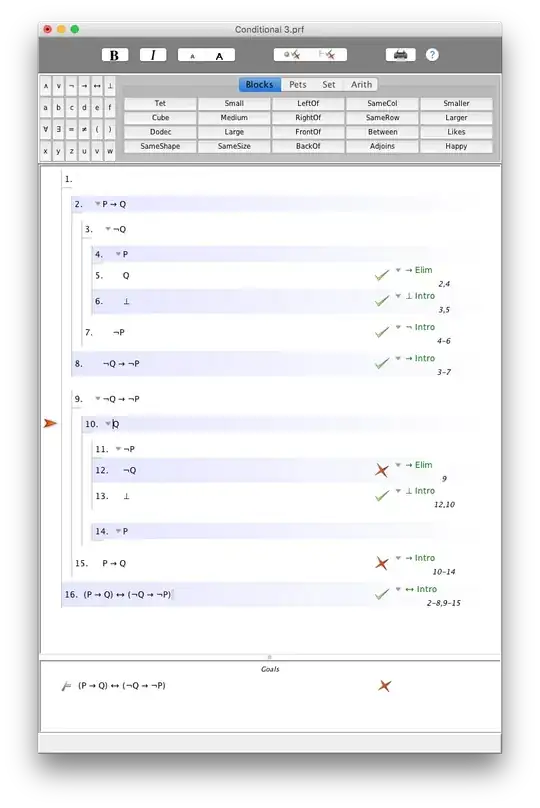
Fitch is correct.
First, you are falling for the formal fallacy affirming the consequent in your subproof at 11-13 to generate the contradiction. Denying the antecedent looks like:
- A → B
- B
- Therefore, A
In your case ,
- ~Q → ~P
- ~P
- Therefore, ~Q
Second, you are discharging the subproof incorrectly. At 10, you assume Q, but at 15 you discharge as P → Q. Instead, (if the inside were accurate), it would be Q → P.
If instead, you use modus tollens instead of affirming the consequent, you can reach your proof. Modus tollens is:
- P → Q
- ~Q
- Therefore, ~P.
Spelled out more directly:
10. | | P
11. | | ~~P DN 10
12. | | ~~Q MT 9,11
13. | | Q DN
14. | P → Q CP 10-13
Fitch might not have MT. In which case, you can prove it:
- A → B
- ~B
- | A Assumption
- | B MP 1,3
- | ⊥ 2,4 ⊥ Introduction
- ~A 3-5 ¬ Intro