1

Does the dissonance of scale notes, to the tonic, follow a pattern of ascending fifths?

For example start with a C major scale and lets track the position of the C note in ascending keys ... C G D A E B etc.

In key of C, C is at position 1.

In key of G, C is as position 5.

In key of D, C is at position 2.

In key of A, C is at position 6.

In key of E, C is at position 3.

In key of B, C is at position 7.

In key of F#, C is at position 4#.

(I am using 5# instead of 5b as we're ascending.)

The resulting pattern is 1-5-2-6-3-7-4#.

This means that the 4 must be on the other end ...

4-1-5-2-6-3-7 ... then

4#-1#-5#-2#-6#-3#-7# ... etc.

(And this pattern follows if we had descended.)

4b-1b-5b-2b-6b-3b-7b ... then

4-1-5-2-6-3-7 ... then

4#-1#-5#-2#-6#-3#-7# ... etc.

(In this manner one might say key signatures 'start' on F, the 4, the beginning of the grouping, and not C.)

Regardless, the question is, does the 4-1-5-2-6-3-7 also denote the dissonance of the scale tones relative to the I?

Is 4 (F) the most consonant to C?, then 5 (G), then 2(D) etc?

Randy Zeitman
  • 2,151
  • 1
  • 7
  • 27
  • Related: [What is the list of intervals in order of dissonance](https://music.stackexchange.com/q/46509/21766) – Richard Mar 14 '19 at 16:51

4 Answers4

3

No, the 4-1-5-2-6-3-7 does not denote the dissonance of the scale tones relative to I (at least not strictly).

While both 4 and 5 are quite consonant with 1, 6 is more consonant with 1 than 2 is, as 6 creates a 6th or a 3rd, while 2 creates a 2nd or a 7th.

Using your example, F (4) and G (5) may be among the most consonant with C (1), but A (6) and E (3) are both more consonant with C (1) than D (2) is.

Dekkadeci
  • 12,898
  • 2
  • 26
  • 52
2

It's difficult talking about the circle of fifths without a cirlce so I made one...

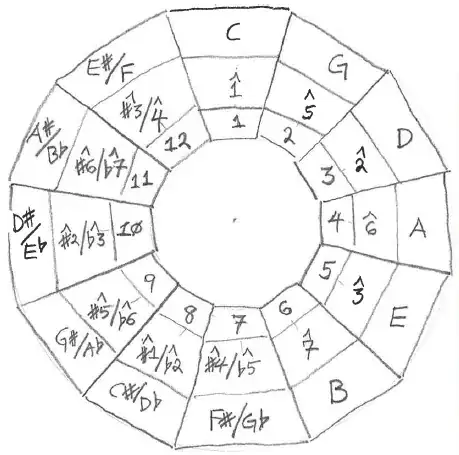
enter image description here

Coincidentally, I was thinking about one of the concepts in this question only a few days ago: if you want to generate the major scale from the circle of fifths, you need to go back one step on the circle from a starting position tonic to get the ^4 scale degree.

Of course you can also say that if you just go up seven steps from a starting tonic position you will end on a #^4 and have the Lydian mode. (Look into The Lydian Chromatic Concept of Tonal Organization by George Russell. Apparently he thought this particular rooting of a segment of the circle of fifths was the way to organize tonal music.)

You can take this idea further and step back further on the circle to get all the modes. This is the chart I made for myself to illustrate the idea...

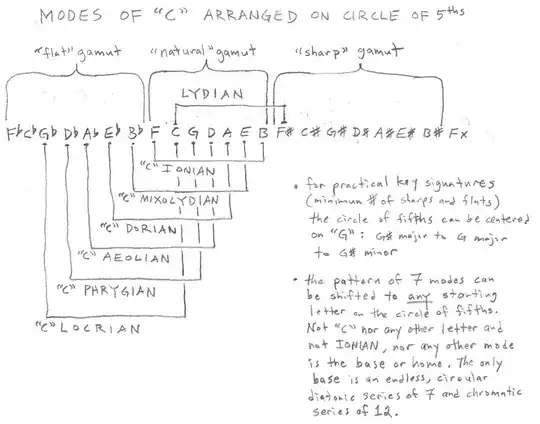
enter image description here

The conclusion I came to was any series of seven adjacent steps on the circle will produce a diatonic tone set and you can then select any one of those tones to be a tonic to create any of the seven modes. Therefore, to select any one particular scale from the circle is totally arbitrary. You can't use the circle of fifths to claim the major scale is the center, nor the Lydian mode, nor any other.

That's a long way to get to the first point which is scale degree sequences like this...

1-5-2-6-3-7-4#

...when applied to the circle of fifths are arbitrary. You can make C any scale degree you want. I can simply say C isn't ^1 but instead it's #^4... of Gb Lydian.

Putting scales degrees arbitrarily on the circle of fifth seem to just obscure the real question.

The degree of dissonance of any scale degree against the scale tonic will simply be the degree of dissonance for the interval between the two tones. The circle of fifths has nothing to do with it.

Is 4 (F) the most consonant to C?, then 5 (G), then 2(D) etc?

Even if we say for the sake of argument that the circle of fifths position does determine dissonance of a scale degree, F and G are the same distance from C how could one be more or less dissonant based on circle position? They would be equal.

This question seems to be one of a series that tries to find the inherent dissonance of individual things. (At least that's how I've been reading between the lines.) B supposedly would be very dissonant and that kind of matches up with the leading tone being a tendency tone. But then E should be the next most dissonance. However, E is the mediant, a stable scale degree. This idea seems to conflate scale degree characteristics, tendency tone behavior, and dissonance.

Along similar thinking, if we compared the perfect fifth C G and A E the first is closer to the tonic than the other. Does that mean the first perfect fifth is more consonant than the second perfect fifth. That doesn't seem to make much sense to me.

This search for inherent dissonance kind of reminds me of Charles Rosen's ideas about structural dissonance in that both go beyond viewing dissonance/consonance as a quality of intervals. But grand ideas like that seem to require a sophisticated theory. Rosen qualifies the meaning. It's not simply dissonance it's structural dissonance. It's clear that he meant to create a new concept... and he wrote a lot to explain it.

Associating a scale degree to a series position and then calling it simply 'dissonant' strikes me as a very incomplete concept.

Michael Curtis
  • 53,281
  • 2
  • 42
  • 147
  • I don't understand why you're involving CG vs. AE. In the question it's simply asking if the notes are more dissonant to C (or perhaps F) as one does to the right. You wrote a lot about your own explorations but didn't seem to address mine. – Randy Zeitman Mar 14 '19 at 17:47
  • 2
    Your idea is very incomplete. I took it a few steps further to see where it logically leads. I do think I addressed your question: you cannot measure dissonance in the way you propose. – Michael Curtis Mar 14 '19 at 17:50
  • ?... if you say it's incomplete then what's missing? How would you know? Also, why did you start your circle of fifths with C at the top? As you showed in your gamut the C Ionian starts with F ... which makes complete sense to me as keys are built on fifths ... so if you're next key is C then you must go a fifth up from a note that would also be in that following key ... F must be in C. – Randy Zeitman Mar 14 '19 at 22:44
  • 2
    The burden is one you to make a compelling case for your theory, not for me fill in something missing. Basically, I don't think you can make this idea work. I tried to explain that. IMO j ust stick with the standard concepts of dissonance, scale degrees, and tendancy tones, etc. – Michael Curtis Mar 14 '19 at 23:47
  • "Incomplete" and "wrong" are not quite the same. – Randy Zeitman Mar 15 '19 at 02:09
  • I think I figured it out. My math applies to Pythagorean Tuning. – Randy Zeitman Mar 15 '19 at 02:43
  • Hi Micheal, I am making videos about my 'music theory calculator' shortly and I was reviewing this thread I started and saw you use the word 'gamut' instead of what I have ('grouping') and I'd like to use gamut instead. (The dictionary.com thesaurus didn't have gamut as a synonym for group.) The question, any issue with my using 'gamut'? There's nothing else from the diagram I didn't have (see image below, circa 2007). I'd have no issue acknowledging your contribution in the video. http://myeasywebaddress.com/Stage/MusicTheory/permission.jpg – Randy Zeitman Jan 19 '22 at 03:07
  • Hi @RandyZeitman, gamut means the musical letters `ABCDEFG` and perhaps a more modern view would include all transpositions. It's sort of synonymous with "diatonic." If any of this was helpful for your project, I'm glad, but no need to credit me. – Michael Curtis Jan 19 '22 at 15:32
  • Ok, thanks. As I said I’m just using it instead of ‘group’. – Randy Zeitman Jan 19 '22 at 17:21
0

resulting pattern is 1-5-2-6-3-7-

but as we know the order and the degree of dissonante intervals is the 5th,major and minor 3rd and 6th,4th,major and minor 7th and tritonus.

https://en.wikibooks.org/wiki/Music_Theory/Consonance_and_Dissonance

so will find no correlation with the circle of fifths.

(but you'll find other interesting relations and patterns if you search for the augmented triades or the diminished tetrades!)

enter image description here

enter image description here

Albrecht Hügli
  • 25,410
  • 1
  • 21
  • 58
-2

Ok, just found this - dissonance follows the fifths in Pythagorean tuning.

https://en.wikipedia.org/wiki/Just_intonation#Pythagorean_tuning

enter image description here

Randy Zeitman
  • 2,151
  • 1
  • 7
  • 27
  • That chart just states what all the answer have said: dissonance is a relationship between to pitches. B with 243:128 has that complex ratio _only because it's derived from the interval C to B_. – Michael Curtis Mar 15 '19 at 14:52
  • That doesn't mean `B` is the most dissonant note in `C` major, it means the interval `C to B` is very dissonant. – Michael Curtis Mar 15 '19 at 14:54
  • 1
    I really don't get your concept. Are you suggesting that interval `C D` is more consonant than `C E`? You leaping from a tuning chart to a vaguely defined concept of dissonance. Maybe add to your self-answer a few examples of practical application. – Michael Curtis Mar 15 '19 at 15:00
  • 2
    critiquing your posts and comments is *not* rudeness. I've flagged your comment. If you want to participate on this forum you need to be able to accept constructive criticism. – Michael Curtis Mar 15 '19 at 16:34
  • It's worth noting that the other two answers agree with mine conclusion that your concept does not work. I've tried to give you more detail about _what_ the problems are. – Michael Curtis Mar 15 '19 at 16:37