If we say C to E, we say it's a major third since it is belongs to the major scale. If we say C to E♭, we say it's a minor third since it belongs to a minor scale.
What about C to D, F, or G? These intervals are same both in major and minor scales. Do you consider the bass note as the basis for the major scale? (So here we'd consider it C major.)
The word "minor" does not mean the same thing when used to refer to scales and intervals.
A minor interval is a 2nd, 3rd, 6th, or 7th in which the upper note is one semitone lower than its major equivalent. It does not necessarily mean it is part of the minor scale.
In your example of C to Eb, the interval is minor not because Eb is part of the C minor scale, but because Eb is one semitone lower than the major equivalent E.
When finding interval quality, you use the bass note as the root of the major scale, and find what note the top note would be in that scale. Then you find how many semitones lower or higher it is to find its quality. You always find the difference from the major scale.
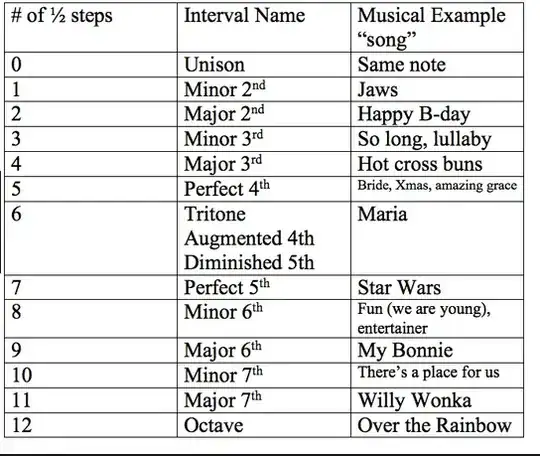
You're confused - and rightly so! It would appear that your assumption is correct, in that C>E is a maj3, found in a major scale, and C>Eb is min3, found in a minor scale. It just happens that way. 2nds, 3rds, 6ths and 7ths all have 4 different flavours. dim., min., maj., and aug. The 4ths and 5ths have 3 flavours, dim., perfect and aug.
A second, C>D is called a maj.2, a third, C>E is a maj.3rd. make those intervals smaller by a semitone, they're minor, smaller by a tone and they're diminished. Make the major interval bigger by a semitone, it's augmented.
The 5ths can only be a semitone smaller (dim.) or a semitone bigger (aug.)
Intervals are found initially by the name of the two notes, counting from the lower. Thus - C>E=maj3; C>Eb=min3; C>Ebb=dim3; C>E#=aug3. Finally, if you take C>F, it's a perfect 4, but if that F note is actually technically E#, then the interval is aug3, not P4. So, we don't, and can't, use no. of semitones as an absolute criterion.
...And another thing! Intervals couldn't be realated to scale notes per se. There are three minor scales, so for instance, the 'seventh' in the natural minor is m7, while the 'seventh' in harmonic is major 7. How could those facts relate to whether a scale is major or minor...
And yet another! To help understand intervals, try inverting them. Majors become minors, and vice versa, while augs become dims, and vice versa. Perfects stay perfect. The 'rule of 9' applies. So, inverse of m3 = M6. inverse of M7 is m2. Inverse of P5 =P4. Give it a try, it may help make sense, where logic sometimes isn't the best.
First, I will answer the question in your title: can you find an interval and define it [based on the scale in which the interval occurs]? The answer is definitively "no." The names of intervals do not always match the names of the scale in which those intervals occur.
To illustrate this, let's compare a few different C scales:
C Lydian: C D E F# G A B
1 2 3 #4 5 6 7
C major: C D E F G A B
1 2 3 4 5 6 7
C Mixolydian: C D E F G A Bb
1 2 3 4 5 6 b7
C Dorian minor: C D Eb F G A Bb
1 2 b3 4 5 6 b7
C natural minor: C D Eb F G Ab Bb
1 2 b3 4 5 b6 b7
C Phrygian: C Db Eb F G Ab Bb
1 b2 b3 4 5 b6 b7
C Locrian: C Db Eb F Gb Ab Bb
1 b2 b3 4 b5 b6 b7
C harmonic minor: C D Eb F G Ab B
1 2 b3 4 5 b6 7
C melodic minor: C D Eb F G A B
1 2 b3 4 5 6 7
These are just some of the scales we could write down. When we consider all of these different scales, something becomes clear: it doesn't make sense to define an interval based on the scale in which the interval is found, because there's simply too much overlap. We cannot require a minor scale to contain only minor or diminished intervals--this would produce an altogether different scale from what we know as minor. Indeed, this overlap is easy to see. For example, a major second interval (C to D) is found in all of these scales: major scale, minor scale (all three types), Lydian scale, and Mixolydian scale. We don't call this a "Lydian second" or a "Mixolydian second." We simply call it a major second (as opposed to giving it multiple different names).
You might be wondering "what is the convention for naming intervals?" This would be a different answer altogether and might be worth asking in a separate question.
You've got it half right! Yes, the major and perfect intervals may be defined as the notes of the major scale that starts on the lower note. But we can't be as glib about minor intervals.
Forget about minor scales for now. We name intervals according to their relationship to the notes in the major scale starting on the lower note.
One basic concept. Semitone (or Fret) counting won't do. This is part of the language of notation and harmony and, in a language, spelling matters!
Another basic concept, KNOW YOUR MAJOR SCALES.
Consider the major scale starting on the lower note of the interval:
Is the upper note in the scale? If so, the interval is called Major (for 2nds, 3rds, 6ths and 7ths) or Perfect (for 4th's, 5ths and Octaves/Unisons).
Is it one semitone up from there? It's called Augmented.
One semitone down? If it's one of the 'major' bunch it's called Minor. If it's from the Perfect bunch it's called Diminished.
Two semitones down? There's a step below Minor called Diminished. Nothing for 4ths 5ths and Octaves/Unisons. They go straight from Perfect to Diminished. There's no special name for the interval two semitones smaller than a Perfect 4th, 5th or Octave. (Well, none that's of any practical use. I suppose you could invent something like 'double-diminished.)
THE SPELLING MATTERS. The note 3 semitones higher than C might be spelled Eb, it might be spelled D#. The former is a Minor 3rd above C, the latter am Augmented 2nd.
And that's about it.
In a broader musical context, minor and Major can mean different things. When we speak of scales we can say a Major or minor scale. When we speak of chords we have a Major chord which is a set of notes a Major Third and a perfect fifth from the root note.
In this case, we have to do with intervals. A Major interval is a space between two notes where both notes fit in the Major scale of the root. C - E is a Major third because C major has an E natural for the third note of the scale.
This is just the short hand for how we teach people to get to the interval. This does not mean that this interval has all that much to do with the scale we are in.
C-E remains a Major third regardless of the scale. It is the interval in C Major, it is the interval in F Major and the interval in G Major. You could say that the intervals are key agnostic.
...is it based on major and minor keys?
No. To clear up this part of the question consider this. C and E also belong to A minor, but we don't call the interval a major third.
If we say C to E♭, we say it's a minor third since it belongs to a minor scale.
No. You could also say C and Eb also belong the B flat major, but we don't call the interval a major third.
How do we do it?
We don't get the interval name by its relation to a scale, key, or chord. Instead, we get the interval only by comparing the two notes in a a two step process.
First the interval is measured in steps of the staff letters A to G. In this example C is one (or a unison), D is the second, and E is the third. Our basic interval is a third.
Next we determine the quality of the interval by measuring in semitones. Thirds that are 4 semitones apart are major thirds. C natural to E natural is 4 semitones apart and so is a major third. C to Eb is 3 semitones apart and so is a minor third.
Wikipedia has a good, full description in its article on intervals.
Correct interval naming really involves reading from a score or understanding conventions about key signatures and harmony. It can also be confusing when dealing with enharmonic equivalents. Be prepared to grapple with those issues if you dig in deeper.
You are confusing the concept of scale qualities and intervals.
C to E is not called a major third because it is from the major scale. By definition a major third is 4 half steps from any note to any note regardless of scale.
In E minor there is a major third between C and E even though it belongs to the minor scale... in fact a C major chord C E G belongs to F major, C major, G major, D minor, A minor and E minor.
To answer your question:
C to D is a Major 2nd
C to F is a Perfect 4th
C to G is a Perfect 5th
C to A is a Major 6th
C to B is a Major 7th
So you're wondering why you see no minor intervals in the major scale? You do.
E to G - minor third... or how about A to C... D to F... all minor thirds. Just depends what note you start from.
Let's breakdown all the intervals
NOTE: a semi-tone is the same as half-step)
Credit goes to westrowanmusictheory.weebly.com for this picture
