Why do two identical notes never cancel each other out?

Question

If we consider a note as a sine function with a certain frequency (ignoring timbre), if you start playing another sine function, even with the same frequency but starting at a different offset, assuming the result is just a sum of the individual waves, we could even get complete destructive interference and get no sound. What misconception do I have about sound?

Answer 1

If you play two sine waves of constant amplitude at the same frequency, then the result will be another sine wave. If your two sine waves are in phase, then you have a louder sinewave. if your two waves are completely out of phase, then the result will indeed be silence.

It sounds like you're observing that two notes played with a slight offset don't typically cancel each other out like this, and trying to reconcile that with the fact that two sine waves of constant amplitude could so easily cancel each other out. I think the thing to take away is that a typical instrument sound is very much more complex than a sine wave. If you were to consider (say) a piano note as a sum of sinewaves, each of those sinewaves can be thought of as constantly changing in pitch and amplitude; it's almost impossible for all of the sinusoidal components to be totally out of phase for any period of time, which is why you rarely hear two played notes cancelling each other out. They can still cancel somewhat, which gives you a comb filtering effect - this is exactly how phasing and flanging effects work.

In a three dimensional acoustic space, if two notes are played in different locations, there's also a different summation that reaches each ear, which further reduces the chance of complete cancellation happening.

Answer 2

I think the other answers underemphasize the number one factor why this doesn't happen in real life - phase. For this to happen, both waves need to arrive at your ear precisely in phase AND STAY THERE.

Well, actually, they don't even need to be precisely 180° offset for you to notice effects. Partial cancellation would be pretty noticeable too, and I think that even different timbres, if they were properly synced, would produce a noticeable distortion. But it doesn't happen. Because:

Check out this picture of ripples in water that I picked up from Google:

Note that there are multiple sources of waves and the waves travel outward in circles. And there are indeed places where the waves intersect and cancel each other out. But because each wave started at a different location, these spots ALSO move around.

And that's your problem: unless both sounds emanate from precisely the same spot, their waves won't cancel out. There will just be a few spots where they do, but these spots will move around and never stay in the same place.

Now, there might be some locations where the effects might be more noticeable - for example on the line connecting the two centres. But again - we're talking about a veeeery fine line here. And that's without taking into account all the echoes that normally happen in real life.

So, in other words - yes, two waves of the same frequency CAN noticeably interfere with each other - but the stars need to be aligned JUST RIGHT for that to happen.

Answer 3

If we consider a note as a sine function with a certain frequency (ignoring timbre), [...] What misconception do I have about sound?

You consider a note as a sine function with a certain frequency. Notes have beginnings and endings (including attacks and decays), sine functions don't. Notes have overtones with characteristic phase relations, sine functions don't. Notes have disharmonicity, sine functions don't.

If you ever tried localising comparatively clean mains hum, you'll know that sine functions in isolation are a beast to deal with regarding hearing. You'll have no problems whatsoever locating a double bass playing a prolonged G1 or B1 (sort of the closest notes to mains hum depending on your locale). A bassoon will still be pretty locatable. A wooden open organ pipe of "flute" type, in contrast, will be rather tricky with those notes, as will a bass ocarina.

Multiple such instruments with that kind of almost pure sine tone quality are rather elusive to locate which is the reason that many speaker setups use only a single subwoofer. Higher frequencies, in contrast, have overlapping sound fields that you can tap into pretty well by moving your head.

PA systems actually have rather large problems for systems with multiple speakers to ensure there are no significant sound extinctions in the listening area: that's a science in itself. So clearly identical frequencies don't do you the favor to generally add without extinction occuring.

Answer 4

There are some good answers here, but I was surprised that there were no visualizations of the actual waveforms yet, nor quantitative answers, which I found to be a very intuitive way of understanding what was going on.

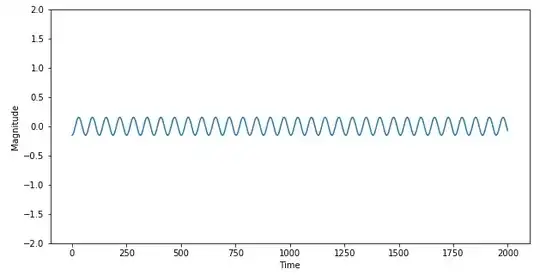
If we have a sound at 440Hz (A above middle C on a piano), that means that the sine wave of that sound is oscillating 440 times per second. One way of thinking about this is the waveform over time (if we imagine we have a perfectly idealized sine wave, which as other answerers have noted, is impossible):

440Hz per second means that a professional Silent Pianist would need to time his or her second node to the troughs of the wave; if you wanted to pick a particular trough to play against, you'd only have error bars of 2.3 milliseconds to execute your cancelling keypress before the next peak was beginning. If you just want a trough at random, you can press the note again any time the piano wire is in a trough. But you still need to be quite exact: You not only need to play at exactly the same volume as last time, but also at precisely the trough of the wave, not a moment sooner.

Here's what the waveform looks like if you're just a few milliseconds off:

Diminished, to be sure — but still audible!

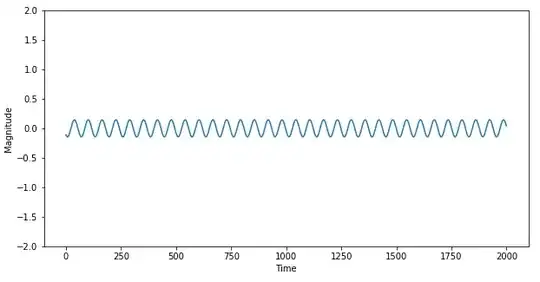
Here's what it looks like if you somehow manage to time everything perfectly, but your second note is just 1% louder than last time:

In other words, even if you have 99% accuracy in timing and in volume (or even 100% accuracy in one but not the other), you still won't be able to manage to cancel out a tone.

What if conditions change and the wire is a little warmer the second time you hit it, or the air density around the wire has gone down, or the hammer hits a slightly different place on the string? (These sorts of small variations happen every time you play a note!)

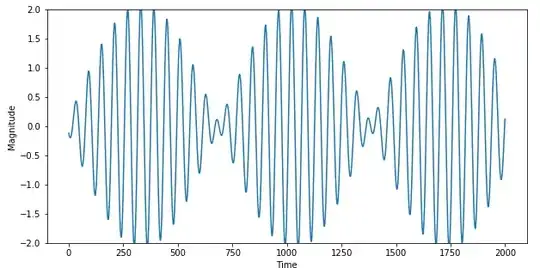
Here's the same waveform, but now with an offset in the frequency of the second note press:

This oscillation is because the relative time between constructive and destructive interference changes with time!

This is the closest that a human could likely come to cancelling out a sine wave in real life: And if you hold two sine wave speakers near each other and move them around, you will indeed manage to hear this "wowowowowowow" sound characteristic of this oscillation, due to the differences in mass and resistance of the two speaker drums.

Do note, however, that this is a very unpleasant thing to do :)

Answer 5

The sounds do interfere with each other, producing sounds called "beats". Piano tuners, for example, listen for both the presence and absence of beats in determining if two pitches are in tune with each other. Some pairings should produce beats, others should not. And instrumentalists do the same thing when tuning their instruments to each other.

At the same time, human hearing has the ability to differentiate sounds. If a relatively small number of sounds are heard together, one hears them — are learns to hear them — as distinct pitches. However, play too many simultaneous sounds that interfere with each other, the ability to differentiate is overwhelmed. For example, laying one's arms across a piano keyboard and playing all the covered pitches at once, will produce a mass of indistinguishable sounds.

What we call "white noise" is similar: so many different frequencies, that it all just becomes auditory mush.

Answer 6

Sine waves can cancel each other out completely because of the oscillatory symmetry of the waveform: the portion of the cycle during which the pressure decreases is the mirror image of the portion during which the pressure increases. Therefore, the wave being 1/2 cycle out of phase is the same as the wave being inverted. That is, shifting the graph to the right or left is the same as mirroring it on the horizontal axis. (For that matter, mirroring the graph around a vertical line yields an equivalent result to a phase shift.) The same property holds for square waves and for triangular waves.

The fourth waveform typically used in additive synthesis is the sawtooth wave, and this property does not hold for such waves. Similarly, if you look at the waveforms of actual musical instruments, they do not possess this sort of symmetry. Consequently, a phase shift does not result in an inverted waveform.

(Another factor, mentioned elsewhere, is that the phase of a sound wave at the listener's location depends on the distance from the source, so even for perfect sine waves, some locations will experience destructive interference while others experience destructive interference. There is an animation at https://en.wikipedia.org/wiki/File:Two_sources_interference.gif. Note the radial lines where the color remains constant. No tone is heard there.

Answer 7

They WILL interfere, forming a new complex signal. However, for it to really be noticed, the brain needs to be able to draw simple inferences. Total sound cancelation of out-of-phase sine waves is one example of a VERY noticeable effect, but there are others.

A flanger is a very good example of creative use of small delays, and is very noticeable.

Related, I suppose, would be the idea of INVERSION of sound, as in noise-cancelling headphones.

Answer 8

From a real-life perspective, If you have identical recordings of perfectly symmetric waves over the zero crossing, like sine waves, and you manage to play them exactly at half period asynchrony times to add the + and - sides to a zero, the volume will be zero.

In reality, waves are mostly not symmetrical and the timing is very precise to get symmetrical waves to play at exactly opposite phases, that you only can substract two waves if you set it it up precisely in the machine...

With human-precision timing, it's rare to have silence from two exact same waves of symmetry over zero, and with normal waves, which are a bit irregular, it's impossible to have silence, but it's possible to have a few dB of attenuation.

You'd also have to have two notes coming from the same speaker to cancel out, because two notes coming from different places are like waves in a pond, even if they are the same amplitude, they only converge and cancel out in specific places.

Answer 9

Why do two identical notes never cancel each other out?

They do. And if they're absolutely identical when they hit the ear, they cancel completely. (Not that this often happens. Nothing's 100% in real life.)

This is a practical issue with synthesisers and sequencer programs. If they generate exactly the same waveform when instructed to play the same note twice, something that can easily happen in polyphonic music, there can be a considerable amount of cancellation resulting in a weak, 'hollow' sound. Even when the issue is addressed by adding a bit of variation to repeated notes, we still don't build a violin section (orchestras typically have 8-12 1st Violins playing the same music) by creating 8 instances of the same Violin instrument, we use a single instance of a 'Violin Section' patch. The effect is also used in noise-cancelling headphones.

So I'm afraid your question is invalid. They do!

Answer 10

In practice, pure sinewaves are extremely rare. Most sounds have significant harmonics in them. So when the fundamental is cancelled out, the harmonic an octave higher is reinforced. It's well known that your brain will fill in the bass when harmonics are played together (for example when you hear a major chord which has a 4:5:6 frequency ratio.)

There are only 2 instruments that I can think of that deliver a really pure sinewave. One is a tuning fork. When first struck it rings with a higher frequency harmonic but that quickly decays leaving a pure sinewave. This is beause the energy of any asymmetric vibrations is carried to the handle and dissipated in the flesh of your hand, leaving only the symmetric vibration where the two tines move in opposite directions. If you hold one of the tines to your ear you can hear it. Rotate it 90 degrees about the handle so the space between the tines is to your ear and you will hear a sinewave 180 degrees out of phase. In between these two points, at about 45 degrees, the tuning fork is inaudible, because the sound from the outside of the tine and the space between the tines cancel out.

The other instrument is a synthesizer. Use of slightly different frequency sinewaves is used in the intro to "Kick it In" by Simple minds. As the sinewaves merge in and out of phase you can hear the note beating in a way that familiar to anyone who has tuned a stringed instrument. However, unlike a stringed instrument whose sound contains harmonics, when the sinewaves are out of phase the note is completely silent.