7

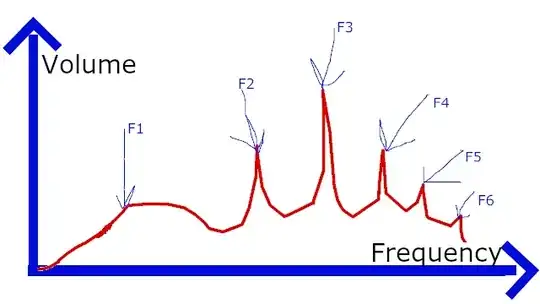
because when I press for example on a piano key, that I trace the spectrum of the sound, I have this (amplitudes in function of frequencies) enter image description here Question: how to define the fundamental frequency of the note? Is this

  • A) F0 because it is any sound emitted the lowest (less than 1 Hz)

  • B) F1 because it is the most serious peak, even if the peak is rounded

  • C) F2 because among the highest peaks (only the very high peaks are taken into account), it is the most serious

  • D) F3 because it is the strongest peak

user33894
  • 71
  • 2
  • There is a related Q&A at the Digital Processing SE: [Finding pitch from a wideband spectrogram](https://dsp.stackexchange.com/q/414) – Aaron Jun 15 '21 at 17:26
  • Regarding rounded peaks, consider that most frequency plots like this have a log scale for the frequency axis. This is useful in a music production context, since the low end is where things tend to get crowded and muddy, making more resolution there valuable. It does, however, tend to skew the perspective of the 'strength' of each peak, as peaks will get wider and shorter on the graph at lower frequencies for the same peak width in absolute frequency terms. – Dan Bryant Jun 16 '21 at 02:04

2 Answers2

6

If we assume that this is a harmonic sound (which is a good enough assumption for pianos) and that this is a spectrum of only one note being played, then the fundamental frequency n will be the highest frequency such that F1 = a1n, F2 = a2n, F3 = a3n, ..., where a1, a2, a3, ... are all positive integers. (In other words, n is the greatest common divisor of F1, F2, F3, ...)

For example, if we were given a plot with F1 = 200Hz, F2 = 300Hz, F3 = 500Hz, F4 = 600Hz, then we could say pretty confidently that the fundamental is 100Hz, since the peaks are at 2*100, 3*100, 5*100, 6*100.

One way to make a guess at n is to look at the difference between two peaks (e.g. 600Hz-500Hz = 100Hz). There's a pretty good chance that this will be the fundamental, but you have to go back and verify that your guess is right... It's possible for tones to be missing harmonics (The example I gave here is missing the 400Hz harmonic, so you might guess that the fundamental is 200Hz, which is not right).

(And if you were given a plot with F1 = 201Hz, F2 = 297Hz, F3 = 499Hz, F4 = 602Hz, you would conclude that the fundamental is still 100Hz but there's some measurement error, or the tone isn't quite perfectly harmonic... Most of these plots are not precise enough for tuning)

Edward
  • 6,015
  • 1
  • 10
  • 46
  • 1
    It's not uncommon for the even harmonics to be missing, in which case the fundamental is half the difference. – phoog Jun 15 '21 at 18:57
  • 1
    This is a good answer in that it gets to the heart of what makes a harmonic sound harmonic. The only thing missing IMO is the phrase "[greatest common divisor](https://www.wolframalpha.com/input/?i=gcd+200%2C+300%2C+500%2C+600)". – Theodore Jun 15 '21 at 19:21
  • Essentially, I used a definition of "greatest common divisor"... But yes, I'll add that term in here. – Edward Jun 15 '21 at 20:14
  • I think this previous answer has links to a more accurate formula taking into account inharmonicity using for example string tension and width https://music.stackexchange.com/a/112009/60885. – Emil Jun 17 '21 at 05:55
  • @Emil The inharmonicity for the first few harmonics of a piano is low enough that it's just not worth solving a few fourth-order differential equations to find the fundamental. Never mind the data collection required to fill in the coefficients... – Edward Jun 18 '21 at 04:44
  • @Edward: I think it was just a corrective factor with a square root and some material properties, no need to solve PDEs. – Emil Jun 18 '21 at 10:22
2

Your diagram is not very well drawn and I would refrain from drawing a conclusion based on it. That said, it does look like your higher frequencies are evenly spaced.

Your descriptions of F0 (non existent) and F1 (serious?) are misleading. Why is F1 "serious"?

You also claim that F2 is highest and F3 is "strongest", what's the difference? High = strong in spectral analysis.

Based only on the data provided you may not be able to tell what the fundamental is. Perhaps you have 6 distinct fundamentals created by pure tone generators.

You state that this is a piano key being played. Each key in an acoustic piano strikes 3 strings, so there is no way you are going to get a pure spectrum for a single string. Of course the multiple strings are tuned to complement each other and reinforce harmonics.

In general, the fundamental would be the common difference between the peaks in the sequence. It looks like F3-F2 = F4-F3 = F5-F4 = F6-F5 so I would say that this is the fundamental. Just based on appearances this delta does NOT line up with F1 so I can't tell if that is the true fundamental.

It is rather common for harmonics to be missing so you may need more information that just consecutive differences to determine the true fundamental.

Also, it is very common for higher harmonics to be stronger than the fundamental so the strongest peak should never be assumed to be the true fundamental. In fact the brain has a signal processing feature called fundamental tracking that will cause a listener to hear the fundamental even when it's missing as long as there is enough data in the harmonics present for the brain to determine a common delta.

  • 1
    Although most keys on a piano correspond to 3 strings, the F1 key will have only 1 or 2 on most pianos. – Aaron Jun 15 '21 at 22:07
  • Thank you. I knew most had more than one but I'm not that well versed on piano construction. –  Jun 15 '21 at 22:12
  • The question doesn't actually claim that F2 is highest, only that it's among the highest peaks. – psmears Jun 16 '21 at 13:22
  • But it then claims it is the most serious, not among the most serious. Very confusing. –  Jun 16 '21 at 14:08