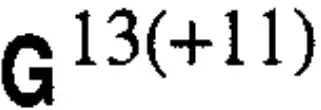Does an altered 9th/11th/13th imply the full tertian stack?

Question

This is a chord symbol notation question. When an extension like 9, 11 and 13 is added to a triad chord symbol but has an alteration (flat or sharp), does it still imply the seventh and lower extensions?

1. For example, would C #11 (if there is such a thing) mean C E G F# or C E G Bb D F#?
2. If C #11 isn't valid, how would both chords above be notated? C(add#11) vs C9(#11)?
3. Is there a difference if it is notated as C(#11) or are the parentheses only to prevent misreading the chord as C# 11?

Thanks!

Answer 1

I think this needs to be answered from the conventional point of view rather than logical, because jazz chords symbols provide a logical system, but conventionally people don't always strictly follow the system.

A good example is dominant ninth chords. G9 would be a ninth chord and the seventh is understood to be in the chord despite it not being written out. I think that is mostly an issue of visual formatting. If you just wrote G79 it looks funny... a seventy ninth chord?!?. G7(9) is cumbersome, so the shortened G9 is used. Then, for some reason, altered ninth chord will include the 7, example G7♭9. There doesn't seem to be a logical reason to not simply write G♭9 - G(♭9) to clarify the flat. It seems part of the convention is to avoid writing parenthesis. Drop the 7 to avoid parenthesis, but other times include the 7 to avoid parenthesis.

Logically G#11 should be understood as a G dominant seventh chord with a sharp eleventh added. But it seems the conventional symbol is G7#11. Why?

I think the reason is because the #11 is associated with lydian and that brings a different tonality than major/minor with blue notes.

If you look for the diatonic chord, in major, that has diatonic sharp eleventh, an augmented fourth, it's the IV chord. In C major that would be F A C E G B, with the B being the "sharp eleventh." But notice that the seventh is major. To write that in jazz you need to specify the seventh: FΔ7♯11. That is a lydian chord.

There is also the lydian dominant chord & scale which is a form of the melodic minor scale. That scale has its own special tonal identity. Conventionally the chord symbol, for an F root, is F7♯11. Logically you would drop the 7 and just write F♯11. But I think the convention to include the seventh is probably to make the distinction between the two important lydian types.

I don't think the same kind of logic versus convention comes up with 13 chords simply because ♯13 and ♭13, because a sharp thirteenth is enharmonically a minor seventh, and a flat thirteenth ends up sounding like a different root, i.e. Cm7♭13 sounds more convincing as the inverted A♭Δ9/C.

Answer 2

There are various chord notation conventions. A decent reference can be found in Aebersold Free Handbook, p. 15 (https://www.jazzbooks.com/mm5/download/FQBK-handbook.pdf).

Several notes:

• chord symbol C#11 means a chord with C# as a root, flat 7, natural 11. If you wanted C7 with sharp 11, you should rather write C7#11. For C with major seventh and sharp 11 write Cmaj7#11, CΔ#11 or similar.
• note that chord symbols are often not interpreted literally. If you want a musician to play the exact six notes: C-E-G-Bb-D-F#, write it down in a score. Otherwise they will likely omit some of the notes, maybe also add others, maybe even add alterations according to their taste and what they hear is happening in the band.
• natural 11 is typically considered an avoid note in major chords, thus C13 will rather be interpreted as C7 with natural 9 and without 11. If you want both 13 and 11, you should rather write C13(11). I have never seen such chord symbol used.
• Sometimes people choose to add parentheses in the symbols, but most often they are only for additional visual clarity, and omitting them wouldn't change the meaning of the chord symbol, see e.g.:

An exception could be the mentioned above C13(11) which would look really weird without parentheses, but it seems to me like an academic example.

Personally I actually find symbols without parentheses easier to read. Note also how much visual clarity can be created by placing the alterations in two lines, as in the B7#9#5 above.

• The chord symbols given in each line of the handbook are very frequently synonymous to each other. E.g. Em7 can be often interpreted as Em9 or Em11, unless e.g. the underlying scale is E-phrygian (because e.g. we're strongly in the key of C), then natural 9 wouldn't fit.
• In general the handbook is a good and very practical reference, but I have some remarks: 1. for locrian natural 2 I prefer symbol Cø♮2 rather than Cø#2, as the latter might be ambiguous (is it natural or raised 2?). 2. Slash chords are typically notated with a diagonal slash e.g. G-/C, rather than with two symbols on top of each other (which is sometimes used for stacked chords). I feel like those two style elements are from old times and are avoided in more recent publications.

Answer 3

I think because the culture of jazz is so improvisational, jazz notation should be as precise as possible (if that's what you're after). A vague chord symbol gives the instrumentalist room to interpret the music how they like. If you see C(#11), I think the specific voicing is left intentionally up to you. If you just want the 11 without the extra extensions, I think a more clear way to write that would be C(add #11).

Sometimes you may need to be very specific to avoid clashes between rhythm and horn sections. If you write C7, a pianist may add a 9th just for fun. If you really don't want them to have fun ;) , you should specifically write C7(no 9th). That's why often times you'll see huge symbols like C7b9(+5).

I think parentheses don't have any specific meaning; however, they can make the symbol more reader friendly. When sight reading C# 11, you might accidentally see that as C #11. Something like C#(add 11) would be more clear.

In practice, chord symbols can be notated a lot of different ways. Usually, the publisher will format all their music to their own "house rules" for consistency.

Answer 4

It's a sort of dupe - the other question concerned only about 'standard' extensions - diatonic ones, if you like. (I'm not including ♭7 here!!).

The fact that 9th, 11 and 13 are altered doesn't change the 'stacked thirds' concept. Even flattening or sharpening the 5 retains that idea. There is always the option to leave out certain chord components, for reasons given in the answer to the other question.

The 7th should always be retained when the chord number is greater than 7, and sometimes the 9th is left out of an 11 or 13 chord - obviously not if that 9th itself is altered!

So, in say, a ♯11 chord, the 7 must be present, but the 9 is optional. Being ♯11 doesn't affect any other notes except that ♯11.