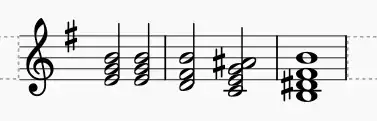For the chord C7 (specifically!), why do you write B♭ and not A♯?
-
2This has already been answered here https://music.stackexchange.com/questions/23976/why-do-notes-have-multiple-names. We should not need a new answer for every chord and scale. – Dom Dec 15 '20 at 22:54
-
It also looks like your question is more on the lines of : https://music.stackexchange.com/questions/11189/why-is-a-c7-chord-named-a-dominant-seventh-chord – Dom Dec 15 '20 at 23:01
-
If you haven't already, please have a look at Dom's alternatives - they may or may not be dupes, but they certainly give many interesting angles on your question. – Tim Dec 16 '20 at 10:38
-
@JohnBelzaguy - that much is true! BUT - which scale notes should one use? It's confusing that C7 actually *doesn't* use the scale notes of key C..! – Tim Dec 16 '20 at 10:40
-
@Tim - The C7 chord is not in the key of C, it is in the key of F (which has a Bb). It *can* occur in a C major song but, even then, it usually signals a temporary change of key to F. – chasly - supports Monica Dec 16 '20 at 14:52
-
@chasly-supportsMonica - did you read my answer? C7 can occur in just about any key available. And usually heralds an F. Except in Blues, but that's a different kettle of fish. – Tim Dec 16 '20 at 14:55
-
@Tim - So I don't understand why you say "It's confusing that C7 actually doesn't use the scale notes of key C". It isn't confusing at all in my opinion - it's because it is using the scale of F major, not the scale of C. If you use the scale of C you get a different chord - Cmaj7. – chasly - supports Monica Dec 16 '20 at 15:00
-
P.S. Here are the natural chords in the key of C: **C / Dm / Em / F / G(7) / Am / Bdim** and here are the natural chords in the key of F: **F / Gm / Am / Bb / C(7) / Dm / Edim** - The added notes for the seventh chord are always in the key of the Tonic scale. That is why we don't have to specify "flattened 7th". – chasly - supports Monica Dec 16 '20 at 15:12
-
@chasly-supportsMonica - what I'm trying to say is that C7 has far more to do with key F, as you say. For years, I thought of it as 'from the key C', which is obviously incorrect, but since it's called 'C something', that puts it, in some people's thoughts, as it's more to do with key C than any other. I think we agree, but it seems I'm struggling to explain clearly. Certainly agree that it doesn't need 'b7' justifying, which seems to be the essence of a lot of answers here. – Tim Dec 16 '20 at 15:19
10 Answers
The "C" part of the chord's name tells you that the chord's root (or 1st degree) is C. This means that the letter part of the name of its 7th degree is B. (Counting from the 1st to the 7th degree: C D E F G A B.) This applies to any sort of 7th-chord whose root is C. C7 means a C major triad with a minor 7th, and, as Tim pointed out, the note a minor 7th above C is B♭.
Don't know if this tells you something you didn't already know, but here goes:
"C7" designates a C major chord with an added seventh interval. Here a "minor seventh", it would become a "major seventh" if you played the B natural with the C major, widening the interval by a half-step.
You will find that the notes C and B, are seven steps apart, counting "1" on the C. Even if a B flat (B♭) is at issue here, the number assigned to an interval (seventh/third/fifth/etc.) comes from counting the letters, corresponding to the white keys on the piano, in order: "C D E F G A B".
Why call it a C7 chord and not a "C augmented 6th", though — which would warrant calling the note A♯ instead of B♭? (six letters counting from C to A. (To be sure: These chords, built as simply as possible, are all the exact same keys on the piano. Regardless of what we call them.)
Because: Music in the Western world has a fundamental practice of building chords in thirds on top of each other. C D E F G A B. Skipping one letter, as I have done in bold type here, gives the interval of a third every time, C to E, then E to G, and so on. Thus we arrive at a B — whether that is a natural B, or a flattened one — by taking the process of building a C major chord just one step further. This happens all the time, because of thirds being stacked onto eachother all the time to make chords. Therefore, basic three-note chords "with a seventh added" happens all the time, and is more theoretically fundamental than chords with added 6ths.
-
1Thank you so much, this really helped! "Why call it a C7 chord and not a "C augmented 6th", though — which would warrant calling the note A# instead of Bb? (six letters counting from C to A", this really explains it all right there in a very simple way! :) – Sofie Dec 15 '20 at 18:19
-
4@Sofie It's important to note that the chord names were created to describe chords that already existed, not the other way around. All the theory mentioned in these answers existed before the chord symbol "C7" was invented, so they used what fit. In traditional harmony, augmented intervals resolve up (A# to B) and sevenths resolve down (Bb to A). So calling is "C augmented 6th" just doesn't make sense in the system. – Peter Dec 15 '20 at 19:49
-
I meant at first to write in my answer: because A is the 6th degree and Bb is the 7th. – Albrecht Hügli Dec 15 '20 at 22:45
-
@Sofie Another point to consider is that every letter must appear exactly once in the scale. In a scale that already has an A, calling the following note A# would violate this rule because there would be two A-named notes and zero B-named notes. In a C aug 6 chord, the A is sharped rather than the B being flatted, but both letters still appear in the scale. (The scale notes would be ... G - A# - B ... rather than ... G - A - Bb ...) – GalacticCowboy Dec 16 '20 at 19:54
-
@Sofie the augmented sixth chord is very common, actually, though in jazz it's usually spelled as the enharmonically equivalent dominant seventh chord. It's simpler to stick to one spelling, and this spelling is consistent with the idea of stacked thirds (which has been carried far beyond anything reasonable in my opinion). Because it's spelled as a dominant seventh chord, jazz theory calls it a tritone substitution instead. – phoog Dec 17 '20 at 03:35
-
1@Peter it makes sense to call it C augmented sixth if the next chord is B-something, though. – phoog Dec 17 '20 at 03:37
-
@phoog No, it still wouldn't work because "augmented sixth" don't exist in this style of chord symbol notation - there is a symbol for C7, but no symbol for C augmented sixth. The German, Italian, etc augmented sixth chords belong to the world of roman numeral analysis. Two different systems for identifying chords, but mixing the systems can cause confusion (as we see). – Peter Dec 17 '20 at 04:18
There is a formula for writing notes and intervals in the major scale as well as those that appear in any chord.
In any key the letter names of the notes of the major scale in order of appearance are a 7 character (or 8 if you include the octave), unbroken, sequence from the string...
{..., A, B, C, D, E, F, G, A, B, C, D, E, F, G, A, ...}
Appropriate sharps and flats need to be added to get the correct intervals {w, w, h, w, w, w, h} between consecutive notes. The naturally occurring steps are all w = whole with the exception of {B, C} and {E, F} which are each h = half.
The C major scale is {C, D, E, F, G, A, B, C}.
The A major scale letter names are {A, B, C, D, E, F, G, A} and to get the correct steps we need sharps --> {A, B, C#, D, E, F#, G#, A}. The accidentals do not change the letter names.
We also refer to the notes by degree, which is just an integer indexing the location of that note in the scale. For the major scale the degrees are always {1, 2, 3, 4, 5, 6, 7, 8}. So the 2nd degree of C is D while the 2nd degree of A is B. Degrees are universal in some sense.
The chords are constructed from consecutive 3rds, or every other note in the scale.
Some formulas for chords are as follows:
Major = (1, 3, 5)
Minor = (1, b3, 5)
Maj 6 = (1, 3, 5, 6)
7th = (1, 3, 5, b7)
etc.
Applying this to C one gets the following.
C Maj = (C, E, G)
C min = (C, Eb, G)
C maj 6 = (C, E, G, A)
C7 = (C, E, G, Bb)
Simply put B is the 7th degree of C and the formula mandates that this note be a flattened 7th, rather than a sharp 6th.
The reason you asked is probably because you are familiar with enharmonic notes. In the 12TET tuning system the frequency of an A# is identical to a Bb, in all keys. This is why equal temperament was invented. In other tuning systems these notes are not the same frequency. To ensure consistency across all spellings of a chord form we have adopted these conventions. A "7th" chord is (1, 3, 5, b7) and should be spelled as such in any and all keys. A Bb7 is (Bb, D, F, Ab) for example. A Gb7 would have an Fb even though this is also enharmonically equivalent to an E. I used to get points off on music theory quizzes in high school because I'd just through down any whacked out combination of enharmonic names to annoy my teacher.
Extensions of the dominant chord include the 13th, which will have the 6th degree in it. So a C13 chord would be (1, 3, 5, b7, 9, 11, 13), or reduced form might be (1, 3, b7, 9, 13) = (C, E, G, Bb, D, A). Having 2 A's in this would be confusing in terms of function.
- 5,114
- 1
- 13
- 28
The chord C7 comes essentially from the key F. It's the dominant chord in that key. That key contains a B♭, it's in the key signature. There is no A♯ anywhere around, as the A notes in that key are A♮s.
EDIT: The C part is the name of the root. The 7th part refers to the interval that number represents. CDEFGAB. It's an interval of a 7th. But why isn't it CEGB, but CEGB♭? That's in the first part of my answer - it's not from key C - where it could be B, but in key F (where it's from), the 7th from C is B♭. Hopefully this makes more sense than explanations about minor seventh intervals.
EXTRA EDIT: the 'seventh' part of C7 must be a B note of some sort. It cannot be any other! CDEFGAB - 7. So in direct answer to 'why isn't it A♯?' That would make it a C6 of some sort. It's not - it's C7. Now, there are various different sorts of 7ths, the ones emanating from C (major) being the note B♮, the note B♭, and the note B♭♭. The first is called C major seventh, the second C (dominant) 7th, and the last C diminished seventh, all based on the C major triad.Not an A note in sight ! O.K., that diminished looks like an A note, and sounds like an A note, but, honestly, it's a B note - in name. B♭♭.
Spelling C& with an A♯ instead actually makes a C augmented sixth chord - which does sound remarkably similar - identical in 12tet in fact, but because of it being spelt with A♯, it will never be called C7.
- 183,051
- 16
- 181
- 444
-
1Oh okay, thanks for answer - I thought C7 was part of the C major scale at first! – Sofie Dec 15 '20 at 17:21
-
4I would refrain from thinking about C7 as just the dominant chord in F. Yes that is correct, but sticking to explaining as a C chord with a minor seventh stacked on top is a more universal way of thinking about it. In my mind, at least – Andrew the Programmer Dec 15 '20 at 18:37
-
3@AndrewtheProgrammer - both are relevant. Far more people seem to think C7 'belongs' to key C than to key F. I expected other answers to reflect that, but I had a feeling that OP would understand better without getting involved in intervals - which in themselves are mysterious, particularly to beginners. Let's face it, this is more likely to be a beginner's question, with due respect. – Tim Dec 15 '20 at 18:48
-
Nothing against your answer, and to the OP if that makes more sense in your head then don't let me stop you from viewing that way – Andrew the Programmer Dec 15 '20 at 18:55
-
1The point isn't about associating chords to keys, but pitches to roots. – Michael Curtis Dec 15 '20 at 19:04
-
1@Tim: Maybe (probably) it's me, but I fail to see how explaining it by relating it to a key is easier than "add intervals to the root note and adjust". Reasoning by interval yields the exact same result, without involving keys and dominance. – Willem van Rumpt Dec 15 '20 at 19:09
-
-
1The OP has already stated that this answer was helpful, so I'm don't understand the criticism. Chords can be conceived of in multiple ways, and this is a perfectly valid way to learn them. – Peter Dec 15 '20 at 19:52
-
-
-
1OP said they thought C7 was part of C Major, not F Major. The thing is C7 isn't part of *any* scale. It's just a chord built from specific rules. It is *found* in F Major as the dominant, but it could also be used in C major as a transition from the tonic to the subdominant. This makes sense to people who have studied the chords, but to someone new this could be confusing – Andrew the Programmer Dec 15 '20 at 20:05
-
1@AndrewtheProgrammer - the fact that it *is* part of key F *is* the important and relevant point. It can be made in almost any key, but essentially started life in key F. – Tim Dec 15 '20 at 20:38
-
1@AndrewtheProgrammer _no_ chord is part of _any_ scale. Scales are made up of notes, not chords. The phrase "F major" in the sentence "C7 is part of F major" denotes the _key_ of F major, not the _scale._ Chords arose because of *keys,* and pointing out that the dominant seventh chord began its life in functional harmony as the seventh chord built on the dominant is certainly useful for many reasons. – phoog Dec 17 '20 at 03:42
-
1@AndrewtheProgrammer Agreed. Among chord notation systems, the one used here, with roots specified by pitch names, classifies a chord by what *intervals* its notes make with the root. In this system the chord with `A` as root and containing pitches `A C E G` is Am7 or A-7 regardless of whether that's G major's ii7, C major's vi7, F major's iii7 or some chord in another key, or indeed a chord in a passage whose harmony is not functional. The OP asked about a symbol C7 in this notation, so intervals matter here but functions don't. – Rosie F Dec 17 '20 at 08:04
-
@phoog No, there is no concensus whether chords did arise from keys. Relation between chords, keys and scales is (and was) described differently by different theoreticians (also, it's different depending on the perspective, e.g. historical vs psychological). I like the modern tendency to equate scales and chords, so that saying "C7" is the same as "C mixolidean" - it's very practical and has sound psychoacoustic explanation. – fdreger Dec 17 '20 at 12:04
-
@fdreger - interesting, that. Mainly because C Mixolydian is a mode from parent key F. Using exactly the same set of notes. Which is actually where my answer came from. – Tim Dec 17 '20 at 12:24
-
@Tim Explaining music theory concepts often goes in circles. Sometimes we define scales using intervals, and sometimes we define intervals using scales. Much like the classical grammar defines parts of speech in terms of syntax, while the syntax is defined in terms of parts of speech. And unlike mathematics or computer science, where we try to avoid such vicious circles. This particular answer, I feel, is of the ignotum per ignotum variety: to the problem of "why we are not using A# in C7" you reply: "because we are not using A# in F". Quite true, not quite useful. And why no A## in CmM7? – fdreger Dec 17 '20 at 15:18
-
@fdreger I do not claim that chords arose from keys. There is a difference between historical development of music theory (how things "arose") and the current state of music theory (in which the relationship between various concepts may be ahistorical). In the latter, chords are made up of pitches and scales are made up of pitches. A given key will make use of certain chords and certain scales, which may be related, but one does not come from the other, and chords in one key may use pitches that do not come from the corresponding scale. This confuses beginners. – phoog Dec 17 '20 at 21:54
-
@phoog: The exact quote from your comment (that I replied to) was: "Chords arose because of keys". Since now you say: "I do not claim that chords arose from keys", I am a bit confused. Generally, I agree that there is an important difference between synchronous and diachronous description of any system, including music - and (I am not sure what's your stance here) think that blurring lines between those two is often source of much confusion. – fdreger Dec 17 '20 at 22:55
It's because tonal harmony is tertian meaning the chords are built by stacking thirds.
If we look at the two alternate spelling, and root position versus inversions, it should be clearer why using the right enharmonic spelling makes a difference.
When the root is C and we stack up the thirds it's easy to see the first chord is a root position seventh chord, and when inverting the top tone it becomes a third inversion seventh chord...
If the top tones was enharmonically spelled A♯, then on staff the chord looks like a first inversion seventh chord. When the top tone is inverted the chord looks like a root position chord. I say "looks like", but in reality if you spell the chord with A♯, you actually are setting the root as A♯ and the chord's third as C in the tertian system of harmony.
That's really confusing if your intention is a C dominant seventh chord.
When the A♯ is in the bass (remember that's root position) we get a diminished fifth between the root and the fifth of the chord. Immediately we read this is some kind of diminished chord. Looking at all the intervals above the bass we have: d3, d5, d7 diminished third, diminished fifth, diminished seventh. A diminished seventh chord altered with a diminished third enharmonically equal to a dominant seventh chord?!?
The importance of the correct spelling becomes more apparent when you work with harmony in all 24 major and minor key with the full common practice vocabulary of seventh chords and typical chromatic chords.
Sometimes unusual enharmonic spelling are exploited for various reasons like a modulation or a chromatic passage, etc. But if the case is straight forward diatonic harmony like V7 I, then spell the chord in the standard way.
Simple V7 I in F major...
Enharmonic spelling for a chromatic augmented sixth chord to V in E minor...
- 53,281
- 2
- 42
- 147
-
I imagine the OP is not well versed in a lot of what you portray, so it's answering at a different level. In fact, it's somewhat overcomplicated for what is asked! – Tim Dec 15 '20 at 18:51
-
1Maybe. But, partly it's intentional. The second part of my answer _should_ be difficult. The point is if a chord's spelling is difficult and confused, reading it is difficult and confusing. My first example should be followed unless one really intends something chromatic. – Michael Curtis Dec 15 '20 at 19:01
The names and symbols of chords (at least in common practice music) carry harmonic information as well as indicating the notes actually played. Chord symbols are not a variant of tablature (and vice versa.) The symbol, C7, indicates the chord C-E-G-Bb as indicated in other answers. There is the hint that the Bb will move downward, likely to A.
There is a commonly used chord, C-E-G-A# which on keyboards or fretted instruments are the same notes. (For strings and voices and in theory, A# is not the same as Bb; they are called enharmonically equal to indicate the difference. The C-E-G-A# chord is a German Sixth (one of the Augmented Sixth chords) in the key of E.
The important point isn't the names but the resolution of the chords. The general rule is that lowered intervals tend to contract and expanded intervals tend to expand. Also, semitone movent is "stronger" (more noticeable by the audience?) than whole-tone movement. The C7 chord tends to resolve to some form of F chord; the E moves to F and the Bb moves to A. Other tones follow voice leading rules. (In 4-part harmony, dominant seventh to tonic movement isn't easy.) Thus the German Sixth resolves outward C-E-G-A# goes to B-E-G#-B (and then to B-D#-F#-B with another half-step movement in the E-D# move.)
The point is that a performer whether playing from music, memory, or just making things up as it goes, can tell from the name or symbol what is likely to come next. Traditional notation carries lots of information.
- 24,207
- 1
- 31
- 76
I had this confusion too for a long time, so I thought I might add my two cents and state what I haven't seen stated explicitly. That is, it is because of a convention brought about for historical reasons that are no longer relevant.
However, with modern music theory, the convention has actually turned out to be useful for other reasons. But it is nonetheless a historical accident.
The convention is this:
For all common 7 tone scales, it is a convention that we use all letters from A to G exactly once.
This is relevant because when we use numbers to denote chord extensions (such as the 7 in C7, or in Cmaj7), what we are saying is that we mean the nth note in some scale. So for your example of C7, it is assumed that we are using the dominant scale with root C, and that the 7 means the normal C major, but add the 7th note of the scale.
When we take into consideration the convention of using all the notes A to G exactly once, the dominant scale is spelled C D E F G A Bb; it is not spelled C D E F G A A#, since the latter would break the convention. Our chord is therefore C E G Bb, and not C E G A#.
But I find it important to note again that it is only convention.
But we keep the convention for two reasons
It is hard to break such a long standing and old convention
It has proved to be useful for communicating the context of the chord.
The second reason is more relevant than the first, so I will elaborate on that one.
As mentioned earlier, saying C7 brings with it a certain scale that the chord is assumed to be built on, that is, the dominant scale. This communicates immediately that the function of the chord is a dominant one, since there are no other modes with a major 3rd and a flat 7th. In other words, if you are reading a well written piece of sheet music, and you see C E G Bb, you can know that whoever composed the song is probably communicating to you that they mean to use this chord to lead into the next chord.
This means, that if you are, say, improvising, or coming up with your own arrangement of a song, you can easily come up with more ways to alter the chord to express yourself without sounding off. As long as you keep that function of leading into the next chord, you can substitute almost any other chord and it will probably sound okay. Any voice leading that sounds like it very strongly leads into the next one will probably sound fine.
If say, you saw C E G A# in a well written piece of sheet music, then you will assume that the composer means to communicate something different. This may communicate, for example, that they are building off of the regular C major scale, or maybe some more exotic scale like C D E F G A# B, (not sure what its called, but playing it sounds very bluesy, and not as random as you might think), in which the chord may actually have a tonic function, and thus, again, if you were arranging or improvising, you might be thinking more "tonically" when substituting or improvising over this chord (common in blues).
Of course, this is all fairly hypothetical, and you will often see a dominate 7th chord denote a chord with a tonic function as well (such as in a blues progression). So really, it is convention, albeit a somewhat useful one for communicating context and intent.
- 295
- 2
- 8
-
1"For all common 7 tone scales, it is a convention that we use all letters from A to G exactly once." could be an answer all on its own. – Wossname Dec 16 '20 at 23:06
-
"dominant scale"? I know what you mean, but this is not a standard concept in music theory as far as I am aware. Also, your second paragraph seems to imply that enharmonic equivalence was invented at some point, but that's not really true. A sharp and B flat were the same note before they weren't (that is, there were 12-tone keyboards before there were split-key keyboards). – phoog Dec 17 '20 at 03:47
-
@phoog You misunderstand about the 12 tone keyboards. Yes, there were always 12 tone keyboards, but different keys denoted different tunings for these 12 tone keyboards since equal temperament was not in common use until actually fairly recently (relatively speaking). Before equal temperament, the differently spelled notes in different major scales would actually sound different because they were tuned differently, and music notation developed with that in mind (i.e. assuming that you couldn't really modulate keys), until Bach made well temperament more popular. – William Oliver Dec 17 '20 at 10:43
-
@phoog Moreover, It is slightly uncommon to hear the term "dominant scale" but it is not a term that I made up. Its common enough that it has a wikipedia disambiguation and is referred to here https://en.wikipedia.org/wiki/Mixolydian_mode#Modern_Mixolydian (read the third line of that section). I just thought the term Mixolydian mode might be more confusing for explaining the dominant chord than it needed to be. – William Oliver Dec 17 '20 at 10:46
-
@WilliamOliver A sharp and B flat are the same on a 12-tone keyboard no matter how it is tuned. Twelve-tone keyboards in meantone tuning are limited in their ability to modulate, but it is not impossible. Do you imagine that Buxtehude retuned the organ between the movements of Membra Jesu Nostri? I do not, and I do not think that he had split keys. Bach did not make "well" temperament popular; he capitalized on its development, as did others in those days, only not as systematically as Bach. – phoog Dec 17 '20 at 22:43
-
@phoog This is stated more explicitly in this video at 10:44 https://youtu.be/TgwaiEKnMTQ?t=642 When they were invented, Sharps and flats were used to denote the sharps and flats in the mean tone tuning, and thus A# and Bb would probably not have been considered same thing. However, to be fair, the specific comparison between A# and Bb may never have come up in practice, but meantone tuning is nonetheless a major reason for the existence of #s and bs in musical notation. – William Oliver Dec 18 '20 at 05:01
-
@WilliamOliver that video describes practical compromises one must make when using meantone temperament. It doesn't say anything about notation. Though the A♭/G♯ key (to be more realistic) has one pitch or the other assigned to it, it was still used for both despite being ill tuned for that purpose. The existence of large-scale works with movements in both flat and sharp keys implies that this was the case by the late 17th century, before Bach's birth. In fact there is a school of thought that large-scale motion from flat to sharp keys was designed to capitalize on the tuning differences. – phoog Dec 18 '20 at 15:22
-
As to the reason for sharps and flats in music notation, that can be explained without any recourse to tuning systems. From antiquity it was recognized that some steps in the diatonic scale were roughly half as big as the others. As the Guidonian system of notation evolved during the middle ages and the Renaissance, eventually any whole step could have a note in the middle, which was a sharp if the melodic motion was upward or a flat if it was downward, because that's the only sensible way with staff notation. The tuning terminology followed from the notation, not the other way around. – phoog Dec 18 '20 at 15:29
-
@phoog I was wrong about Bach in my above comment. I see now that this is a common misconception. But the point still stands, at their inception, sharps and flats were closer to their base notes than they are now. The connection between the tuning and the notation can be found here https://en.wikipedia.org/wiki/Accidental_(music)#History_of_notation_of_accidentals As you say, "large-scale motion from flat to sharp keys was designed to capitalize on the tuning differences" meaning, they knew about and capitalized on this asymmetry between flats and sharps. – William Oliver Dec 18 '20 at 15:32
-
@phoog The point being that in this system of notation, mean tone tuning (or pythagorean tuning) was assumed. This is a result of equal temperament being extremely difficult to tune correctly for the average person until fairly recently. – William Oliver Dec 18 '20 at 15:40
-
@phoog I think maybe part of the confusion is that I probably should not have said different keys denoted different "tunings", by this I did not mean a different tuning _system_. I meant that when you apply the pythagorean/mean tone tuning system to two different base notes, you will end up with different frequencies for the notes. – William Oliver Dec 18 '20 at 15:44
-
Let us [continue this discussion in chat](https://chat.stackexchange.com/rooms/117423/discussion-between-phoog-and-william-oliver). – phoog Dec 18 '20 at 15:50
The seventh chord is built from the 1st, 3rd, 5th, and 7th step from the root note. That seventh interval has to be a minor seventh. In C7, this would be C D E F G A Bb. Huh???
I'll add a snippet of knowledge by starting with the importance (and difference) of quality and distance in intervals. An interval is just two notes, and when we go to measure, we have to think about how far they are apart, and which notes to use to write them down.
Which notes we use to write them down is the distance. For example, C to E will always a third, C to F will always be a fourth, and C to B will always be a seventh, no matter how many accidentals you attach to either notes. You find this by first converting everything to regular natural notes and counting what step the top note is in relation to the root one
Quality is a bit trickier. It evaluates what the descriptor for the distance. We can agree that C to Eb and C to E are both a third, but they are clearly NOT the same. In this case, you have to memorize the order the difference between minor and major (and perfect, diminished, and augmented, but let's not overcomplicate now) intervals. For a seventh to be minor seventh, it has to be five whole steps away from the root, and respectively for a major seventh it has to be 5.5 whole steps away
Back to C7. Since we know it's a seventh, we know that the two notes are C and some form of B. That's our distance. The B then has to be flatter because we want to make it a minor seventh to satisfy the quality of the chord. A#, though it would an enharmonic equivalent, would make it a augmented sixth, and that would be a completely different chord theoretically
- 996
- 5
- 15
Because C,E,G,A is C6 (and A# would be C +13) and not C7. (The 7th degree belonging to the C scale is B and not Bb)
C7 = V7 of F! It stands for the dominant 7th chord C,E,G,B♭ => so,ti,re,fa of the F keys.
- 6,448
- 16
- 36
- 25,410
- 1
- 21
- 58
Others have given good answers already. (1) There are seven letter names in a scale and each one can be either natural, sharp, or flat. (2) Chord names are aliases for stacks of thirds. But I'll add a practical "test" you can try, to get an intuitive grasp on what's happening with the C7.
Let's say you have this melody line that's played over a C major chord. The melody has the notes: C - B - A - G - C., meaning, 1st, 7th, 6th, 5th, 1st scale degree.
Original melody
Now you want to create a variation of that melody line so that it fits over a C7 chord - what do you do? Compare these alternative melody lines:
(alt. 1) C - B - A# - G - C
(alt. 2) C - Bb - A - G - C
If you play these, it should be immediately obvious that alternative 2 is the correct one, and it reveals the fact that the C7 chord makes the scale's B note flat. It does not make the A sharp.
When you say "A#", it means that your A is sharp. Your 6th scale degree is sharp. By adding the title you say something about your A. It's like saying "Mr. A" or "Mrs. A". You have one "A" slot in the 7-degree scale, and it can be only sharp or natural or flat, but only one of those at any given time.
(The general "wrongness" of alternative 1 can be debated, but if the idea is to modify the original C - B - A - G - C to suit changing the chord to C7, I'd say that alternative 2 can fairly well be called the correct one.)
- 26,045
- 1
- 33
- 85
-
This is confusing. The **wrong** example should show C A# A G as per the original question. Then it becomes obvious that the visual flow of the melody's direction of travel is more easily conveyed in the second example. However, the melody line and the chords assigned are separate things. – melkisadek Dec 24 '20 at 11:16
-
@melkisadek There is no "C A# A G". Your A can be either sharp or natural but not both at the same time. I'm trying to explicate what the scale is. The sixth scale degree is A something, and it cannot be A and A# at the same time. I'm trying to say: if you say "A#", it means that you want your sixth scale degree to be sharp. Which is what was done in the Wrong example. The first note from left is the 1st scale degree. The second note from the left is the 7th scale degree. The third note from the left is the 6th scale degree. The fourth note from the left is the 5th scale degree. – piiperi Reinstate Monica Dec 24 '20 at 12:39
-
@melkisadek If you say "C A# A G", it means that between A# and A, the sixth scale degree is _changed_ from sharp to natural. Do you understand this? And that even during the A# note, it should be possible to use the seventh scale degree B. Try playing C, B and A# simultaneously, does it sound good? – piiperi Reinstate Monica Dec 24 '20 at 15:13
-
The question asks why you write a Bb and not an A# in a C7 chord: (C E G Bb) as opposed to (C E G A#). If I press an A# on a keyboard and then press a Bb I can hit the same key. The question is why do we decide to call it Bb in this case (C7). The answer is that the **chord name** requires the flattened 7th from a root C which is Bb. The question asks why can't the Bb just be marked as an A#. There is nothing in your example which explains why it can't be a sharp 6 **in the case of a C7 chord** where there is no implied A natural. – melkisadek Dec 27 '20 at 01:42
-
@melkisadek My answer is trying to lead into thinking about what the notes of the scale are. What is the 1st note, what is 2nd note, ... what is the 6th note and what is the 7th note. That's why I added the numbers there. A is the sixth note name in the scale, B is the seventh. My examples show what it would mean if the 6th is sharp, vs. what if the 7th is flat. – piiperi Reinstate Monica Dec 27 '20 at 11:38