How can I calculate the rotational force and motor HP needed to lift a 5lb sheet from a horizontal position to a vertical position from one end?

Question

Essentially, I need to know the following:

• How do I calculate the rotation force along a fulcrum? Is there an equation?
  
• What is the weight of a 5 lb object at the fulcrum if the fulcrum is located at Point A (I am assuming Point A is located halfway between the clip attached to the toll gate and the shaft attached to the motor. (See Diagram B.)
  
• What is the unit of measurement for "force"? Newtons?
  
• How can I plug the "force" measurement into an equation in order to find horsepower (HP)? What is the equation?
  
• How much horsepower (HP) is needed in a motor to perform this function?
• If I make the clip holding the 5 lb gate longer, so it extends closer to the center of the gate, will it move the fulcrum and ultimately decrease the workload of the motor? (See Diagram D.)

I drew out a very easy to read picture in Photoshop. I have an idea for something I want to do at home and I need to know what size motor to use.

Please note: The sheet does NOT need to stop the vehicle. The vehicle is there just to make it easier to understand the function. Think of it similar to a lift gate that you go through to pay parking fee in a parking garage.

---

Diagram A: Drawing

---

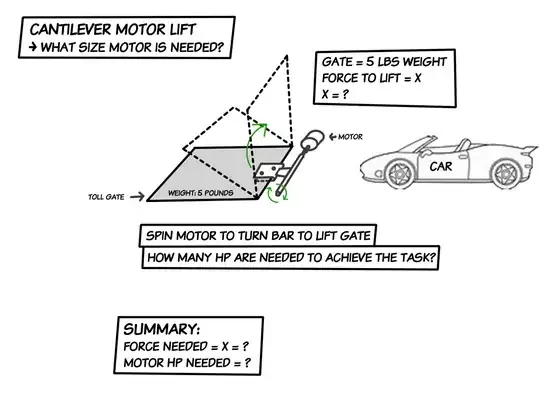
Diagram B: Is This The Fulcrum?

---

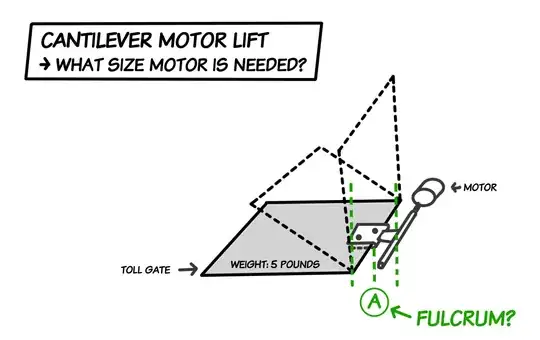
Diagram C: Dimensions

---

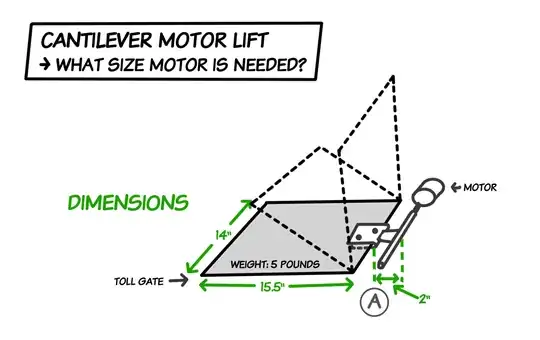
Diagram D: Is This The New Fulcrum Point If Clip Is Extended?

---

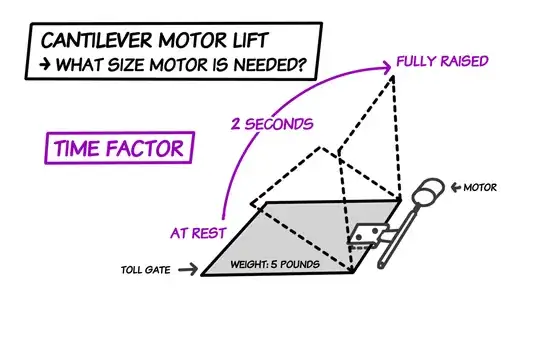
Diagram E: Time Factor - How Long It Takes To Lift

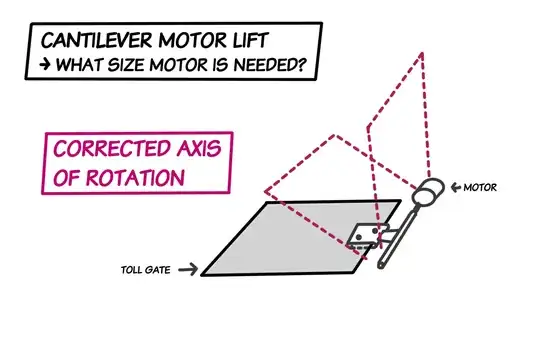
p.s. when I drew the diagrams, I made a small mistake. The axis of rotation is not around the initial point A. To clarify, the axis of rotation is in fact, as you probably suspected, around the shaft directly attached to the motor. In my diagrams, the dashed outline of the movement of the gate is placed along the incorrect axis. I hope this doesn't bother you too much.

Here is a fixed axis of rotation:

---

Diagram F: Corrected Axis Of Rotation

---

Additional Notes:

• I hope that the motor can be a type with a failsafe in which case if the load exceeds a certain amount (like if something heavy was placed on the gate), that instead of burning out the motor, instead it shut off if attempted to turn on.
  
• It must be able to work in reverse as well (let the gate down) as well. Time frame can be slower for letting it down, 3 to 5 seconds perhaps.
  
• Gearbox reduction to be applied & efficiency loss of gearbox? Unknown, Open to suggestions
  
• What type of motor do you plan to use? Open to suggestions
  
• How are you planning to stop it at the vertical? I hope for a combination of gravity and the motor to do the trick.
  
• Is this an operation you plan to do 2 or 3 times or 2 to 3 thousand times? By my estimates, it will be used between 1 and 10 times per day. At even 20 times per day, which would be very unlikely to exceed 20 times in one day, then 20 x 365 days x 50 years will be a nice life span. 365000 operations would be a reasonable case scenario.

---

---

---

---

UPDATE:
BUNCH OF PHYSICS STUFF BELOW:

Based on the following Wikipedia quote, it sounds like that in order to measure the horsepower needed, I need to also calculate the Torque (τ) and Angular Momentum (ω) because the calculations below assume that torque and angular momentum are known.

Wikipedia source - Horsepower

The formula for determining horsepower appears to be:

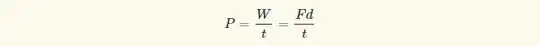
and the final result will be in the form of: 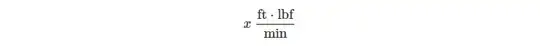where "x" is the unknown variable (tell me if I'm wrong).

If torque and angular speed are known, using a coherent system of units (such as SI), the power may be calculated using the relationship;

P = τω where P is power, τ is torque, and ω is angular speed. When using other units or if the speed is in revolutions per unit time rather than radians, a conversion factor has to be included. When torque is in pound-foot units, rotational speed (f) is in rpm and power is required in horsepower: The constant 5252 is the rounded value of (33,000 ft·lbf/min)/(2π rad/rev).

When torque is in inch pounds:

The constant 63,025 is the rounded value of (33,000 ft·lbf/min) x (12 in/ft)/(2π rad/rev).

Note: The number 33,000 (and hence 5252) exists because: 1 hp = 33,000 ft-lbf/min.
I'm assuming that means the number 5252 is for 1 revolution@1HP (tell me if I'm wrong).

For clarity's sake, in the equations above, from what I can see:

Torque τ = 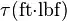, and
Angular Momentum ω =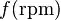

Thus, it stands to reason I must also find Torque (τ) and Angular Momentum (ω) and know their formulas:

---

Torque (τ):

According to Wikipedia on Torque,

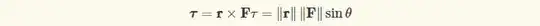
where:

τ is the torque vector and τ is the magnitude of the torque,
r is the displacement vector (a vector from the point from which torque is measured to the point where force is applied),
F is the force vector,
× denotes the cross product,
θ is the angle between the force vector and the lever arm vector.

I do not know how to calculate r, F, sin, or θ.

---

Angular Momentum (ω):

According to Wikipedia on Rotational Speed,

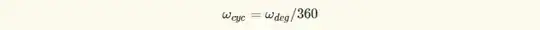
where , is angular speed in degrees per second.

For example, a stepper motor might turn exactly one complete revolution each second. Its angular speed is 360 degrees per second (360°/s), or 2π radians per second (2π rad/s), while the rotational speed is 60 rpm.

Answer 1

Once you have corrected your axis of rotation it should be obvious that the idea to lengthen the "clip" will not change anything with regard to the force required to raise the flap. Actually it could make things worse if the longer clip added more weight to the whole assembly.

The force needed to raise the flap is measured in some units like foot-pounds (ft-lb). In your case the weight of the flap and connecting mechanism is distributed over a distance so the actual formulas to calculate this become in integral in order to solve. You could make a huge simplification and assume that your weight is all at the maximum lever arm distance and this have things over designed but it makes the analysis much simpler. So guess that you have the 5 pounds of flap + maybe 1 pound for the linkages so 6 pounds total. Assume a worst case lever arm of two feet. This means that for simple analysis that you would need a torque capability in 2' x 6lb = 12 ft-lb. That torque can be directly translated to the units that are used by the motor / gearbox combination.

Some general comments about the design.

1) If the overall design as shown is feasible I think you would want at least two if not three mount points to attach the flap to the shaft.

2) You would want to do everything possible to get the hinge edge of the flap as close to the shaft as possible.

3) You should start planning right now for some type of limit mechanism to control the up and down range of travel of the flap. That could range from direct limit switches to physical stops and detection of increased load on the motor when the stops are hit.

4) This type design calls for a gear box of some type to increase the mechanical advantage given to the motor. A worm gear drive can multiply torque a whole lot in a single stage of gearing. A spur gear arrangement may take several gearing steps to keep things in a realistic size volume.

5) Another reason you need a gear box is to reduce the speed of the motor down to a realistic motion speed for the flap. At 2-3 seconds for the flap operating through 90 degrees of operation you can see that for a motor that may want to operate at say 1750 RPM that you are going to need some gearing down. 1750 RPM for some AC motor is ~30 revs per second. Flap is 1/4 revolution in 3 seconds so corresponds to 1 rev in 12 seconds (1/12 rev per second). The gear ratio to reduce this speed is 30 * 12 = 360 to 1.

Now knowing your torque requirement at 12 ft-lb you could estimate that you need a motor of about 1/360 of that torque or about 0.033 ft-lb at the motor. Figure that gear boxes have some torque losses just to operate then so maybe a motor of 0.05 -> 0.07 ft-lb.

Answer 2

@Michael's answer explained how to do the numbers. (I only add that the force required acts as a cosine, the torque required is greatest when you start lifting until it drops to 0 when the plate is vertical)

I will explain how to reduce the force required;

If you add a 12:1 reduction gear then the torque required will be 1/12 of what you need without the reduction gearing. (same with any other reduction gearing)

You can however add some mechanical help to move the plate by for example adding a winch that lifts a weight as the plate drops down and lets it down again when it is lifted. This adds a constant torque that will assist the motor.

You can also use a spring (either a torsion spring or a conventional one using the winch system described above) that assist the motor. This will add a torque that linearly reduces as the plate is raised. With some fine tuning you can make it so both down and up are stable states (no force from the motor required to keep the plate there).