An engine which, in a given position, finds all the possible legal moves, and then selects one of them randomly (each move has the same probability of being chosen) and plays it on the board.
Its rating would very probably be negative. My guess is: around -1500 Elo.
Maybe someone can program such an engine and then make it play against another engine.
We would need to find an engine that would be weak (but it would still be much stronger than our random-engine) and that would already have a known rating. We would then make them play thousands of bullet games, with an increment so that neither engine can lose on time.
The rating of our random-engine can then be quickly calculated.
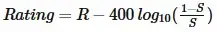
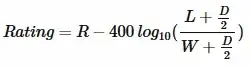
R is the rating of the other engine which served as its opponent. W is the winning probability of the random-engine. L is the losing probability of the random-engine. D is the draw probability. S is the score of the random-engine: S = W + D/2
Notes:
- There is a time increment, and we must assume that both our random-engine and its opponent will never lose on time.
- No player can resign or offer a draw. The game must be played until checkmate, stalemate, 50-move without capture and Pawn movement, or repetition.
- No player can be disqualified by making an illegal move or something like that.
- I am only looking for a very rough approximation, so even if the rating is off by 300 points it would still be good enough.
- Am I talking about FIDE rating, USCF rating, chess.com rating, ICC rating, or some other Elo rating? It doesn’t matter since we’re only looking for an approximation anyway.
- We must assume that the opponent of our random-engine does not know that it is playing against an engine which always plays random moves. Otherwise it would probably constantly threaten checkmate and harass the Queen, or just play ultra-safe waiting for our random-engine to blunder some pieces, which would increase its winning chances even more.