When we draw a general triangle, we're inclined to draw a triangle that's either right, or acute, or obtuse, but not the general triangle itself. Then how do humans know its existence?
-
1Because they can describe it: three points not on the same line connected by three segments pairwise. This allows humans to tell whether what is drawn is or is not a triangle, and to draw images that are. Once they are old enough to understand the difference between a concept and an image, they wouldn't try to *draw* concepts themselves. But this is not what the [problem of universals](https://iep.utm.edu/universa/) is about, it is about the *nature* of general concepts' existence. – Conifold Apr 10 '23 at 07:23
-
2Does this answer your question? [How do humans generalize abstract concepts from concrete objects?](https://philosophy.stackexchange.com/questions/97772/how-do-humans-generalize-abstract-concepts-from-concrete-objects) – Conifold Apr 10 '23 at 07:37
-
TLDR: It's linguistic frippery to say things exist because we can say things exist. Consider becoming a [nominalist (SEP)](https://plato.stanford.edu/entries/nominalism-metaphysics/#Uni) and ending once for all the notion that words make things real. ; ) – J D Apr 10 '23 at 15:31
-
It's a bit misleading to assert that triangles exist when they are mathematical abstractions, so its an ontological question about the existence of mathematical objects which there are many views (see Platonic Heaven). – Richard Bamford Apr 10 '23 at 18:06
-
@Conifold Even this link isn't of much work. It's a good question though. BTW, I saw your comment about Kant's schema. Could you elaborate for me? I guess it's crux to unravel the question. – ploybius Apr 11 '23 at 17:15
-
1It is too complicated to be elaborated here, but I linked two papers that go into details in another comment to that thread. Here are the links, for convenience: [Pippin, Schematism and Empirical Concepts](https://www.degruyter.com/document/doi/10.1515/kant.1976.67.1-4.156/html) and [Pendlebury, Making Sense of Kant's Schematism](https://www.jstor.org/stable/2108332). However, schematism is not about the existence question that you have in the OP, it rather explains how we are able to draw inferences valid for all triangles at once. Whether concept of general triangle "exists" is irrelevant. – Conifold Apr 12 '23 at 00:10
-
@Conifold I find that there is a possible specifc field for this answer, namely mind of philosophy. Does this relate to my question? Also I want to know how concepts are applied to image under condition that there are always slight differences between them – ploybius Apr 15 '23 at 04:52
5 Answers
The general triangle cannot be drawn because it is not a single shape; it is a shorthand way of referring to the common characteristics of triangles as a class of shapes. When we say the general triangle has three sides, what we mean is that all triangles have three sides.
- 8,686
- 1
- 8
- 28
It exists as a set. Now, you may ask : "Have we ever seen that set?". Of course, we have never seen an infinite bunch of things. I would say it's even meaningless to talk about the existence of an infinite bunch of things.
What is meaningful are theories, which are a finite number axioms written in a formal languge. It's the theory of general triangles that exists. I would say that the notion of a general triangle is synonymous with this theory. This theory can be used to deduce the truths about any finite bunch of traingles that you will ever encounter.
Forget the "infinite set of triangles", you will never encounter even a single true triangle in your experience. Even a single triangle is, in principle, characterized by an infinite set of points. Of course, you cannot expect your drawing of a triangle to be a "true triangle", because atoms exist. But what about an imaginary triangle that exists on the continuous manifold of spacetime? Even if we ignore both spacetime curvature and the quantum stuff, there are still big problems with this idea.
Any of our theories of physics can only be tested upto a finite accuracy by doing a finite computation on a finite bunch of things. We have no reason to believe that there exist an "infinite bunch of things" in the ontology of reality. There may not even exist a final model of physics.
In conclusion, it is best to think of any infinite set not as an infinite "bunch of things", but as a theory defined by a finite number of axioms. The utility of these theories is in describing finite sets and finite computations that we actually ever deal with.
- 499
- 4
- 11
-
1
-
@Frank It exists as a string manipulation system that humans can use – Ryder Rude Apr 10 '23 at 13:28
-
Then the question is what sense a string exist? Etc. And this game can be played forever without you giving an adequate notion of existence. – J D Apr 10 '23 at 15:33
-
@JD Existence of course cannot really be defined without going circular. A string manipulation is something concrete that you can actually do in your experience, which is why it exists. A flat triangle as an "infinite bunch of points satisfying certain axioms" is not something you can ever encounter, even if General Relativity and Quantum Mechanics were false. Basically, what I'm trying to do is to avoid Platonism. – Ryder Rude Apr 10 '23 at 16:06
-
I'd say that's an excellent goal. Platonism is a plague on philosophy. So, consider that existence CAN be defined without going circular. It's called an [ostensive definition](https://en.wikipedia.org/wiki/Ostensive_definition). Where the ostensive is inadequate, then the [operational definition](https://en.wikipedia.org/wiki/Operational_definition). Our refuge is in the brute fact and observation consistent with public language. – J D Apr 10 '23 at 16:20
-
+1 "Any of our theories of physics can only be tested upto a finite accuracy by doing a finite computation on a finite bunch of things. We have no reason to believe that there exist an "infinite bunch of things" in the ontology of reality" Rejecting Actual Infinity is righteous. And for the rejection of a final physics, arm yourself with [Hume's argument for inductive fallibilism](https://iep.utm.edu/fallibil/#H6). – J D Apr 10 '23 at 16:25
-
@JD I just tried to give an operational definition by "things you can actually encounter":). Btw can you share why Platonism is disliked in philosophy? I personally just find it unnecessary and try to Occam's Razor it. – Ryder Rude Apr 10 '23 at 16:25
-
Let us [continue this discussion in chat](https://chat.stackexchange.com/rooms/145231/discussion-between-j-d-and-ryder-rude). – J D Apr 10 '23 at 16:31
I will try to use the Aristotelian language to describe the answer.
"when we draw a general triangle" ...
Well, in fact we do not draw a general triangle. We can draw some particular triangle. Even when one imagine a triangle, this imaginary triangle is a particular one.
A definition according to Aristotle have to be by the most close Genus and the especific difference it have. So, one can define a triangle as a polygon with three vertices.
The way the sides of this polygon are arranged are accidental features of the triangle. Like the color of a cat being orange. We all know orange cats are crazy, but the colour is just an acidental feature that exists in the particulars. The essence of a cat is not orange. The essence of a triangle is not be a particular triangle.
- 513
- 2
- 7
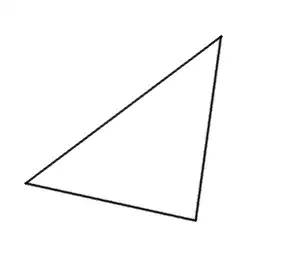
I just drew one. Look.
Neither a right triangle or even an isosceles. Not an "acute triangle" or "obtuse triangle" either, whatever those mean. I know it exists because I can see it.
- 809
- 4
- 11
-
1"whatever those mean": An acute triangle has only angles smaller than 90 degrees. An obtuse triangle has an angle larger than 90 degrees. This is an acute triangle. – MJD Apr 10 '23 at 16:50
-
@MJD I have not heard that terminology before. I guess I'd have to draw a second triangle then. . . . – Daron Apr 10 '23 at 19:23
If you have concerns that universals and abstract objects existing seems nonsensical, like a triangle that exists independent of being scalene, isoceles, equiangular, etc. you might simply conclude that neither universals nor abstract objects in general exist. We can talk of them as if they do exist, and that is useful, but let's be honest, it might grate the mind to act as if triangles are real in the same way a triangular board is, especially devoid of particular properties.
Talking as if they exist but do not is fictionalism (SEP):
Fictionalism about a region of discourse can provisionally be characterized as the view that claims made within that discourse are not best seen as aiming at literal truth but are better regarded as a sort of ‘fiction’. As we will see, this first characterization of fictionalism is in several ways rough. But it is a useful point of departure.
and rejecting abstract objects and universals as a confusion of what exists and what our words claim exists is nominalism (SEP):
Nominalism comes in at least two varieties. In one of them it is the rejection of abstract objects; in the other it is the rejection of universals. Philosophers have often found it necessary to postulate either abstract objects or universals. And so Nominalism in one form or another has played a significant role in the metaphysical debate since at least the Middle Ages, when versions of the second variety of Nominalism were introduced. The two varieties of Nominalism are independent from each other and either can be consistently held without the other.
If you embrace the idea that existence should be rooted in empirical observation, then simply reject the notion that things exists just because someone says they exist. Next time someone says "There exists a thing called a square circle that has both the properties of the square and the circle." Just, say, no it doesn't and you saying it so doesn't make it so. It's a fiction of your language, and then move on.
- 19,541
- 3
- 18
- 83