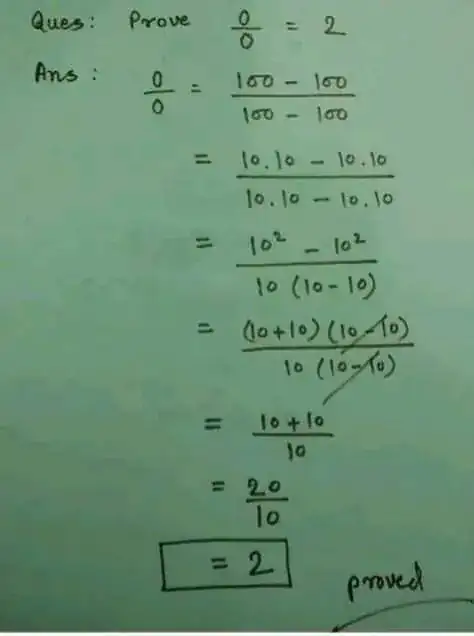-6

I have a "proof" that 0÷0 = 2:

0÷0 = (100 - 100) ÷ (100 - 100)
  = (10⋅10 - 10⋅10) ÷ (10⋅10 - 10⋅10)
  = (10² - 10²) ÷ 10(10 - 10)
  = (10 + 10)(10 - 10) ÷ 10(10 - 10)
  = (10 + 10) ÷ 10
  = 20 ÷ 10
  = 2

It's obviously wrong mathematically (0÷0 is not 2), but this seems like a logically valid proof. Every rewriting step is valid:

  • 0 becomes 100 - 100
  • 100 becomes 10⋅10
  • a⋅a becomes a²
  • ab - ac becomes a(b - c)
  • a² - b² becomes (a + b)(a - b)
  • ac ÷ bc becomes a÷b
  • 10 + 10 becomes 20
  • 20÷10 becomes 2

Is this answer wrong both logically and mathematically, or only wrong mathematically and possible logically? If it's possible logically, does it have any mathematical meaning?

wizzwizz4
  • 1,300
  • 6
  • 17
Wenura
  • 137
  • 6
  • @wizzwizz4: Gah, you're right, don't know what I was thinking! Deleted my comment. – Alexis Jul 24 '22 at 12:48
  • 8
    The derivation fails on the fifth line where you try to cancel "(10-10)" in both numerator and denominator. That would be canceling out an undefined 0/0 term which is not allowed. – causative Jul 24 '22 at 13:11
  • 3
    @WenuraRavindu In line 5, cancelling out 10 - 10 in the numerator and denominator implies you assume that 0/0 = 1. First, you cannot assume any value since you are trying to prove it has one. Second, your assumption that 0/0 = 1 implies that 0/0 = 2 is false. Thus, your proof is inconsistent. – Speakpigeon Jul 24 '22 at 16:07
  • @MauroALLEGRANZA Why did you replace the tags with [tag:reference-request]? It _is_ a [tag:philosophy-of-mathematics] question, despite most mathematicians learning a particular philosophical stance in school. – wizzwizz4 Jul 26 '22 at 14:07
  • 1
    @wizzwizz4 - do you really think that the question about 0/0=2, which is a big mathematical mistake at intermediate level school is a question worth of "philosophical" discussion? Why the OP speak of "logical possibility"? What does it mean? As per comments above he made a mistake in applying the arithmetical "rules of the game": that's all. The purported proof above shows simply why the "official" answer is UNDEFINED: the OP probably didn't notice that the same computation can produce EVERY result. – Mauro ALLEGRANZA Jul 26 '22 at 14:13
  • @MauroALLEGRANZA Yes. Because it's only a mathematical mistake under _certain definitions of division_, and _how we define division_ is a meaningful question. There's more than one way to resolve this; if you're too used to symbol manipulation, you might not remember what it's like to be new to this, and have questions about what it means. (And those questions _are_ valid.) – wizzwizz4 Jul 26 '22 at 14:30
  • Every step is not valid mathematically, there are two steps which you did not justify, the first being that 0/0 is defined (this is asserted by the use of the equality relation, which has as its domain in this context "numbers" ) and the second being that substitution into this expression in the numerator and denominator should behave as it does for division by things that are not 0. These are assumptions, as they cannot be derived from the definition of division, and so this is first error in your proof – Carlyle Jul 13 '23 at 07:42

3 Answers3

5

There is also some Circular Reasoning here, which is straightforwardly a logical mistake, in addition to any mathematical errors.

On line 5, you cancel out the equal divisor and numerator values (10 - 10). What is your justification for this move, given that the purpose of the exercise is determining the value of 0/0?

Paul Ross
  • 5,140
  • 18
  • 37
  • If you assume that cancelling out (10 - 10) / (10 - 10) gives you 0/0, you're instead left with 0/0 = 2×0/0, which suggests 0/0 = 0. – wizzwizz4 Jul 26 '22 at 14:05
  • If you remove the circular reasoning step like that, you still get _a_ value for 0/0. Why is that not a valid thing to do? – wizzwizz4 Aug 13 '22 at 12:16
  • @wizzwizz4, when taking algebraic steps like this, the "cancelling out" effect appeals to an understanding that x/x=1. But if you're trying to make an argument about the value of 0/0, you can't assume that 0/0=1 in the course of your proof. – Paul Ross Aug 13 '22 at 18:16
  • Or, to put it another way, in your edited argument, you have asserted that the step "ac ÷ bc becomes a÷b" is valid for all c, but can you produce a proof for that which includes 0 in the domain of possible values for c? – Paul Ross Aug 13 '22 at 18:20
  • You don't need to turn "ac ÷ bc" into "a÷b"; you can turn it into "a÷b × c÷c" which is fairly uncontroversial. You can then treat 0/0 as opaque (instead of applying the hidden 0/0=1 assumption to cancel it out), and solve for 0/0. However, that still assigns a value to 0/0; either 0/0=0 is valid, or there's another problem with the argument. – wizzwizz4 Aug 13 '22 at 20:03
  • "You can then treat 0/0 as opaque" - do you mean to reduce the equation to e.g. q = 20q/10, then solving for q gives q - 2q = 0 => q = 0? This sounds like it would reasonably avoid the circular reasoning objection, but also is a different argument from the one you presented above. – Paul Ross Aug 13 '22 at 22:15
  • Also, you still need to justify the algebraic relations as correctly applying to a domain including 0. One would assume that it *is* controversial to allow the arbitrary insertion of (0÷0) by means of an algebraic operation. – Paul Ross Aug 13 '22 at 22:20
  • I'm obviously using a different formalism than you; I _thought_ I was giving the same argument as you just said! (q = (20/10) q, but apart from that, the same.) That intuitive understanding of "controversial operations" is one that a working mathematician will pick up, but where does it _come_ from? What _justifies_ it, other than mathematical experience? (That's why I think this is an interesting question; I'm still not sure why it's -5. I wonder whether my edit made it worse.) – wizzwizz4 Aug 13 '22 at 22:30
  • I'm getting a warning about extended comment discussions, but you might find the algebra of Fields a useful starting point: https://en.wikipedia.org/wiki/Field_(mathematics) – Paul Ross Aug 13 '22 at 22:42
3

This proof is disguising a trick that seems like it would work mathematically but actually doesn't. The factoring of the 100 - 100 into different polynomials is just to make the problem seem more valid.

A simpler equivalent would be this:

0 = 1 * 0 = 2 * 0

0   2 * 0
- = -----
0   1 * 0

Cancel the zeroes to get 0/0 = 2/1

The only issue is that you cannot cancel zeroes. This problem just hides that by cancelling (10 - 10) instead. As Speakpigeon said in a comment, cancelling the (10 - 10) would imply that 0/0 = 1, which contradicts the statement that 0/0 = 2.

quixotic
  • 156
  • 5
  • Is very first line of the "proof" not also incorrect, since it states an equality between two expressions that are undefined? (0/0 and (10-10)/(10-10) ) – Carlyle Jul 13 '23 at 07:37
2

As you've noticed, compared to +, - and ×, division is special. There are three schools of thought around questions like this:

0÷0 is undefined

Whenever you try to define it, you end up with a contradiction. Therefore, the division operation is undefined for 0 and 0.

x÷0 is a multi-valued function with all possible values

For every value, you can prove that value is equal to 0÷0. Therefore, it is equal to 0÷0.

What is division, anyway? a÷b means to separate a into b equally-sized groups; when the denominator is 0, there are no groups, so every statement about the group size is vacuously true.

Since it has all values, we don't have a contradiction when we say it has a particular value. Narrowing a multifunction down to a single value is not always a valid thing to do; if you've got a contradiction because you discarded solutions, all that means is you made an algebra mistake.

Here's a simpler example of such an algebra mistake: I'll "prove" that -6 = 0.

  • -3 × -3 = 9
  • Square-rooting both sides, we get √(-3 × -3) = √9
  • √(a × a) = a, so √(-3 × -3) = -3
  • √9 = 3
  • Therefore, -3 = 3
  • Subtract 3 from both sides: -6 = 0

To resolve this issue, we have to either treat define the square root as the positive square root (so √(a × a) = |a|), or treat the square root consistently like a multifunction (√(a × a) = a or -a):

  • -3 × -3 = 9
  • √(-3 × -3) = {-3, 3}
  • √9 = {3, -3}
  • Therefore, {3, -3} ⊥̷ {-3, 3}

0÷0 is defined as having a specific value

Sometimes, it's inconvenient to make division anything other than a total function, so we just define 0÷0 as something, usually 0 or 1. This does mean there are a few algebraic tricks we can't do any more, since they'd lead to a contradiction if we tried to do them on 0÷0.

These different definitions of 0÷0 affect the validity of cancelling out the (10 - 10). Instead of viewing that as a single operation, it might be clearer to think of it as three operations:

  • ac ÷ bc = (a÷b) × (c÷c)
  • c÷c = 1
  • (a÷b) × 1 = a÷b

If these three claims are true, we can "cancel top and bottom". We can prove the third equality quite easily, but the second and (to a lesser extent) first equalities depend on the definition of 0÷0!

  • If 0÷0 is undefined, c÷c = 1 iff c≠0. But, c = 10 - 10, so it's not valid to cancel.
  • If 0÷0 is a multi-valued function, then 1 is always a valid solution for c÷c. However, if c=0, there are other solutions too. Discarding some of those solutions is an extra premise in your argument – or, if you'd prefer, a sloppy argument-by-cases –, and you need to keep that in mind if you end up with a contradiction, because that doesn't necessarily tell you that your original premise was faulty.
  • If 0÷0 is defined as having a specific value:
    • If c÷c = 0, c÷c = 1 if c≠0, otherwise 0. Following your proof with this rule, we conclude that 0÷0 = 2×0, which isn't a contradiction.
    • If c÷c = 1, then the second rule is always valid, but ac ÷ bc = (a÷b) × (c÷c) is only a valid operation when c≠0 or a=b. (This is why I don't like defining 0÷0 = 1; I like the first rule!)

None of these definitions lead to a contradiction.

wizzwizz4
  • 1,300
  • 6
  • 17