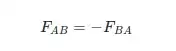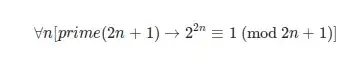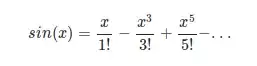6

What's so special or unique about mathematics that we keep coming back to this phrasing?

It isn't universal concision - there are many concepts more concisely put in English than math. Like to show via math the twin experiment isn't paradoxical would require a decent bit of math. But the single sentence "the odometers of two similar cars who start the same and meet the same, but travel different paths will display different mileages" quickly explains a decent portion of the theory. (Obviously there are more details and precision, but this replacement of some portion of math with natural language is the main idea for this paragraph) (Also borrowed this paraphrased example from Tim Maudlin)

Math also isn't universally effective. There are many concepts not easily expressed mathematically like morals, self identity, perception, and emotions.

Math also doesn't exclusively describe anything. There are always other representations (logic, computation, natural language, pictures) for any mathematical formulation.

Lastly, mathematics is not an ontology (unless for radical Platonists). It relays concepts. Well I can undertand a concept in English, French, pictures, diagrams, mathemically equally well if I am competent in those mediums.

To me language is the marvel. And mathematics is a language isn't it?

I'm not trying to be click-baity or reactionary. I just don't see the unique wonder about the "unreasonable effectiveness of mathematics". Language is at least as marvelous, and math is a language. What am I lacking? Am I just being dense?

J Kusin
  • 2,052
  • 1
  • 7
  • 14
  • 3
    More of a side quibble, but the single sentence "the odometers of two similar cars who start the same and meet the same, but travel different paths will display different mileages" absolutely does **not** explain the main point of the twin paradox - that sentence would be true in a purely Newtonian universe as well, but the twin paradox would not be. Separately, re: "There are always other representations," I would include both logic and computation as part of math. – Noah Schweber Sep 15 '21 at 16:32
  • 8
    Mathematics is *not* a language. It *has* a language: the language that mathematicians use to do mathematics. But mathematics itself mostly consists of theories, with axioms, theorems, rules of inference, etc. The language is just used to express these things. – E... Sep 15 '21 at 16:49
  • 1
    NoahSchweber That is true, there's no twin paradox for a Newtonian universe. But just like Galieo's Ship thought experiment and Galilean relativity, some element of a theory could be given a-mathematically. Also edited the phrasing a little to help hopefully. – J Kusin Sep 15 '21 at 16:59
  • 1
    @Eliran I'd call anything that can be translated a langauge. Any mathematical statement could be translated to English, Arabic, or pictures even. – J Kusin Sep 15 '21 at 17:01
  • 3
    Fisrt, people do say that, e.g. [The Unreasonable Effectiveness of Natural Language](https://helsinkicircle.home.blog/2020/03/23/the-unreasonable-effectiveness-of-natural-language/). And second, if we ape for language what Wigner called "unreasonable effectiveness", i.e. that mathematical concepts apply beyond the context where they were developed, there is already a different term for that, [productivity of language](https://plato.stanford.edu/entries/compositionality/#Prod). – Conifold Sep 15 '21 at 18:00
  • "In the first scientific revolution, disputation over the interpretation of human or divine authority was replaced by observation, by measurement, by the testing of hypotheses, all of it with the powerful help of quantitative mathematical reasoning." – David Goodstein, [*The Mechanical Universe*](https://en.wikipedia.org/wiki/The_Mechanical_Universe) - if you grew up watching that you wouldn't question *why math*, as it can represent every concept in the cosmos in no uncertain terms. If you want it in English and with pictures; there it is. – Mazura Sep 16 '21 at 06:09
  • *Any mathematical statement could be translated to English* but not vice versa, because quantitative mathematical reasoning requires observation, measurement, and the testing of hypotheses in a controlled environment. Which is why all sciences testing hypotheses in uncontrolled environments are called *soft*. – Mazura Sep 16 '21 at 06:09
  • 2
    "Math also isn't universally effective" - that would be like arguing that cars aren't an effective form of transportation because they can't drive over water (unless there's some sort of bridge). At best it's just a strawman. "Math also doesn't exclusively describe anything", "mathematics is not an ontology", "language is at least as marvelous" - what does any of that have to do with effectiveness? Just because I can also use a bicycle to get somewhere doesn't mean a car isn't effective. And a car being pretty doesn't make it more effective at getting you from point A to point B. – NotThatGuy Sep 16 '21 at 10:27
  • You should check out https://en.wikipedia.org/wiki/Unreasonable_ineffectiveness_of_mathematics in biology. Einstein said "Most of the fundamental ideas of science are essentially simple, and may, as a rule, be expressed in a language comprehensible to everyone" It feels like you are taking aim against something like Tegmark's 'Mathematical Universe', which I think few here support. Maybe be more explicit. The criticisms are interesting https://en.wikipedia.org/wiki/Mathematical_universe_hypothesis#Criticisms_and_responses I'd call Tegmark's proposal a zombie philosophy of non-philosophers – CriglCragl Sep 16 '21 at 12:24
  • @CriglCragl I'm more of a believer in MUH than most here probably :) It's probably too late to be more specific as this question has run its course I think. – J Kusin Sep 17 '21 at 18:26
  • "I'd call anything that can be translated a langauge. Any mathematical statement could be translated to English, Arabic, or pictures even." Any phyiscs statement could be translated to english, Arabic, or pictures even, does that make physics a language ? Your criterion "I'd call anything that can be translated a langauge" of what constitutes a languge is flawed. Since almost any human intellectual work could be translated into a language, then by your criterion it follows that history, economics, physics, ... are all just languages. – Amr Dec 02 '21 at 11:00
  • @Amr Aren't they "just" languages though? What else are they? Since I am completely unconvinced in any kind of Platonism, I like that math can be treated as ontology-free: it goes if this were true->then this; or treat numbers/sets/categories as if they were true/real then follow their logic. Similarly for a natural language like English, treat solid objects as if they were true/real and use them for your task at hand, don't get caught up in whether solid objects or electrons are really "real". Languages help us solve problems, calling them anything else attaches a metaphysics of some kind. – J Kusin Dec 02 '21 at 15:33
  • @JKusin "Aren't they "just" languages though?" If you consider physics, economics, history, ... as just languages just like English, French,... then you are using the word "language" in a way that's very alien to me. I never encountered anyone before who uses the word "language" like that. By the way even if you adopt a formalist point of view of math (i.e. antiplatonism) it still is different from language, see the comments added beneath my answer. – Amr Dec 03 '21 at 11:53

6 Answers6

5

The effectiveness of mathematics is not only very reasonable but also not fundamentally different from the effectiveness of natural languages. Mathematics is merely the continuation of the conversation we have in any natural languages but using a symbolic notation and presumably a more professional process.

The very reasonable effectiveness of mathematics is entirely down to logic and to the fact that mathematical reasoning is more systematically logical than anything we do in natural languages.

And so now the question is that of the effectiveness of logic itself. A very reasonable explanation then is that logic is a cognitive capacity of the human brain, itself the product of natural selection. This alone is entirely sufficient to justify the fact that logic is adapted to our natural environment and is therefore very effective in allowing us to evolve our beliefs according to our personal experience of our environment. And then there is no reason that this should not apply to more exotic environments as long as we can manage observations of them and thereby obtain reliable data, which is exactly what science does.

Speakpigeon
  • 5,522
  • 1
  • 10
  • 22
  • Thanks @Speakpigeon. Has this always been the predominant view? How recently did it become so if not? – J Kusin Sep 15 '21 at 17:41
  • @JKusin: In my experience, you usually only hear about the "unreasonable effectiveness" of mathematics in response to fictionalist accounts of mathematics, or similar "math isn't real" arguments. It doesn't exist in a vacuum, it's a response to something else. – Kevin Sep 16 '21 at 05:50
  • Concerning the effectiveness of logic: a mathematical point has zero-length, but collections of such points can produce the entire gradation of non-zero lengths, areas and volumes. How is this possible? It’s still puzzling as it was in the time of Zeno of the famed paradoxes, showing that in reasoning about the two basic phenomena of non-zero lengths and moving bodies, our natural mental constructs fail to match actual observations. – exp8j Sep 16 '21 at 09:17
  • The problem is that we cannot visualize actual infinity. But we have to accept it based on what we see. We have invented “infinite series” and “uncountable sets of points” as restrictions in the application of logic, in order to avoid contradictions with the observed facts. Facing these problems with the fundamentals, I think it is very wonderful and “unreasonable” that mathematical physics should exist and flourish. – exp8j Sep 16 '21 at 09:17
  • @JKusin Not, it is not the dominant view. Opinions on the subject are all over the place, and vary according to the academic discipline. The main obstacle to it has been mathematical logic itself, which leads to the idea of a plurality of logics and that logic is arbitrary. – Speakpigeon Sep 16 '21 at 17:40
  • @exp8j "*a mathematical point has zero-length*" There does not seem to be any contradiction in the idea that a region of non-zero area is made of an infinity of zero-dimensional points. This seems to be properly exemplified by the continuity in ℝ of the segment [0, 1] containing an infinity of discrete values and having a length of 1. This is entirely conceptual, though, and does not imply that the real world is like this. It just says that, apparently, it is *possibly* like this. – Speakpigeon Sep 16 '21 at 17:57
  • @exp8j "*in order to avoid contradictions with the observed facts*" No. The use of infinity in mathematics is entirely a pragmatic choice. Logic itself allows infinity, and this presumably because it makes for a more economical neurological processing. – Speakpigeon Sep 16 '21 at 18:05
  • I think this sidesteps the question a little, because theoretical physics typically does not rely on the rigorous logical underpinning of maths but instead involves leaps based on intuition which are often later given a rigorous logical justification. But maybe that's just an argument against the unreasonable effectiveness of mathematics – llama Sep 16 '21 at 18:45
  • @llama Sorry, I don't get your point. – Speakpigeon Sep 17 '21 at 10:33
4

Many aspects of the usefuelness of mathematics are presumably not unreasonable: Things like arithmetic (counting, addition, multiplication etc.) or simple geometry (measurements of length, areas, volumes, angles etc.) were likely developed to deal with obvious real-life problems.

In the same way, our languages evolve to enable us to talk about things that need (or are fun) to be talked about, so it makes sense, and is not unreasonable, that we can discuss concepts and express thoughts in a concise manner. (This is clearly very rough, and the question why or how humans are capable of forming new words/sentences/language constructs (and possibly whether there are general areas which the structure of human language processing makes it impossible or very hard to talk about) is not at all simple.)

On the other hand, the "Unreasonable Effectiveness of Mathematics in the Natural Sciences" usually is thought to mean that purely mathematical concepts turn out to be useful in science, without being developed for that purpose:

  • Formulating laws of nature in mathematically simple form often leads to generalisations that go beyound the initial data but tourn out to be useful.
  • Areas of pure mathematics that were developed without regard to applications turn out to be useful in some area of science, possibly much later (e.g. complex analysis, group theory, non-Euclidean geometry).

I don't see any analogous "unreasonable" effectiveness of language in this sense. (I may just be unaware of them, though.)

Toffomat
  • 150
  • 4
3

I think you have a different definition of "effectiveness" in mind.

Mathematics is effective because it makes predictions that work. If you ask yourself "how far will this cannonball travel", or "will this bridge collapse if 10 cars of weight 1.1t cross it at the same time", you can use mathematical models of physics to get an answer.

I don't see a way to do that by basing your physics on language instead of mathematics. Of course, you can say "this bridge will collapse" and "this bridge won't collapse" with language, but you can't tell which one is correct.

Mathematics and language describe reality on two very different levels.

Federico Poloni
  • 139
  • 3
  • "Mathematics is effective because it makes predictions" That's not mathematics, that's physics. Mathematics operates within definitions, abstractions & assumptions - but makes no comment on whether those are correct ones to have. Is logic language, or maths? Answering that will decide if they are separate – CriglCragl Sep 16 '21 at 14:17
  • 2
    @CriglCragl "Physics makes predictions based on the result of certain mathematical operations", if you prefer, but that does not change my point. – Federico Poloni Sep 16 '21 at 14:18
  • @CriglCragl " "Mathematics is effective because it makes predictions" That's not mathematics, that's physics. ". No, it does make predictions but about formal systems and thats why math is useful in natural sciences. Consider this problem pick any prime p, multiply 2 by itself p times then subtract two. Then divide the answer by p and get the remainder. Evaluating this will take lots of time but doable. Fermat's little theorem makes the prediction that you will get 0 without you having to waste your time to do all these computations – Amr Dec 05 '21 at 08:58
  • math does make predictions but about formal systems and thats why math is useful in natural sciences, let me elaborate on that: Once you have a problem in the real world (say modelling an oscillating spring), then a physicist will pick the model of second order differential equation to model the spring. By doing that the physicist is choosing a problem in a formal system that's equivalent to the real world problem. If you stop at this point, then you haven't made a prediction, – Amr Dec 05 '21 at 09:04
  • @CriglCragl and this is where math comes because you need to make predictions about the problem in the formal system (through numerical methods, taylor series,...etc). So to summarize, what happens is as follows: 1)We have a physics problem 2) We pick a problem in the formal system which we think simulates the physics problem 3) math makes predictions about the problem in the formal system. Both of steps 2) and 3) are necessary to make predictions about the problem we started with which is problem 1 – Amr Dec 05 '21 at 09:06
  • @Amr: No. There are no predictions within pure mathematics, only analytic inferences. It's not a matter for argument, but of terminology. See 'How The Laws Of Physics Lie' https://oxford.universitypressscholarship.com/view/10.1093/0198247044.001.0001/acprof-9780198247043 – CriglCragl Dec 05 '21 at 15:47
  • @criglCragl "It's not a matter for argument," Said who ? Anything can be argued against and I insist to argue against it. "There are no predictions within pure mathematics, only analytic inferences."Yes, this will seem like a reasonable claim to make if the most sophisticated mathematical fact you know is 2+2=4, which is the ONLY example of a mathematical statement referred to in almost all philosophy texts/videos/webpages/discussions I ever came across. Explain to me in which sense is something like Taylor's series for sin(x) is not a prediction ? – Amr Dec 06 '21 at 07:56
2

What's so special or unique about mathematics that we keep coming back to this phrasing?

Math is built on the principle of idealized precision and unambiguity. The value of 1 is precisely 1. It's not 1.0001. That's a completely different value. There's also no other value which is equivalent to 1 in every way. Every value is strictly defined and unique. Every operation is deterministically precise.

Without this kind of precision, math would fall apart by its very threads. It's the equivalent of rounding pi down to be equal to three and then expecting all the subsequent math to still make sense.

From the perspective of someone who enjoys the solidity that such a deterministic system provides (logicians, mathematicians, software developers, ... are definitely a subset of those), human language flaunts these rules constantly. There's ambiguities, partial synonyms, a dependency on contextual inference, a non-universally agreed upon standard, and imprecision is not only understood but also even expected in some cases.

Take the following examples:

Yesterdya I ate an apple

There's a mistake in there, but we hardly stumble over it. If I write this in a book, everyone will know what I mean to convey.

PI = 3.14159265539...

First of all, you're not going to easily spot where I swapped two digits. Secondly, if we take what I wrote at face value, all of my subsequent calculations would start showing inconsistencies, and it would all fall apart.

Using an example from the field of software development to explain how messy humans are: dates.
Humans do reasonably well at understanding dates in daily life and how to make their schedule around them. But the date system is a very human and imprecise one. Inbetween timezones, months of arbitrary length, leap years, exceptions to leap years (and then exceptions to those exceptions, and then ...) DST in some but not all locales, arbitrary holidays that aren't bound to the same date every year and differ for countries and cultures,, timezones with 15/20/30 min differences instead of hourly increments, non-straight timezone boundaries, changes to the standard calendar (julian/gregorian), countries having historically skipped a few days to correct their calendar (IIRC France once skipped 12 days in July to synchronize back to the English' calendar), (let alone relativistic concepts!) ... it is insanely hard to come up with a deterministic system that is consistent and precise.

It is the bane of every software developer's career. If there is a Hell, I imagine it's a place that would make me write the logic that encompasses conversions between all of humanity's timekeeping systems.

It isn't universal concision - there are many concepts more concisely put in English than math

In its defense, this is where the imprecision of human language shines. By being vague and leaving details up for inference, you are able to skip the time-consuming pedantry, instead being able to focus on the broad strokes. Because of math's dependency on absolute precision, it doesn't allow for broad strokes.

A simple example here is that our country has tried to pass a law that lowers the speed limit for trucks when it rains. Simple, clear, understandable. Except that they are unable to enforce this law due to the seemingly infinite ambiguity in "when it rains". How much water should fall from the sky precisely? What about if it stops raining but the road is still wet? How wet should the road be? How could drivers know if the markers for "it rains" have been met while driving? ...

Humans really like building systems that are flexible and malleable so exceptions and inconsistencies can be added whenever there's a reason for them to be there. Mathematics and other deterministic fields abhor flexibility, instead favoring rigidity and extreme consistency.

To a human, math and logic is unnaturally cold and uncaring, devoid of all soul. To a logician, human systems are dirty, messy, and unpredictable.

Flater
  • 1,232
  • 7
  • 8
  • 1
    This helps, and I think highlights one of math's specific traits, it's precision. I've just watched a lecture about Hilbert vs Frege, about if math is "fixed" or not. It seems Hilbert won and math is not fixed to any outside metaphysics. It can "handle" any metaphysics because it is so interally precise and precisely connected to itself. – J Kusin Sep 16 '21 at 15:51
2

"To me language is the marvel. And mathematics is a language isn't it?"

No.

I think I understand where your confusion is coming from. You are thinking of mathematics as merely a tool of description. I wish to challenge your assumption that "math is just a language" in this answer. Mathematics has a language component, which I will denote by L.O.M. (shorthand for language of mathematics). Your problem is that you confuse mathematics with L.O.M. like most math beginners do.

Firstly, what is language ? Language is a correspondence between human ideas/experiences (semantics) and written symbols/spoken sounds (syntax). For example, the human experience of seeing a blue color is corresponded to the written symbols "blue" in the English language and to the written symbols "bleu" in the French language. Note how the same idea (of blue color) gets corresponded to different written characters as the language is changed. Let's have another example, the idea of the number two gets corresponded with the syntax "Two" in English language, gets corresponded to the syntax "Deux" in the French Language, gets corresponded to the syntax "2" in the language L.O.M. mentioned above. Obviously, L.O.M. was designed to have shorter syntax so that the same idea can be expressed more compactly in L.O.M. than in English. In principle any idea that is expressible in L.O.M.is also expressible in English. Take that example:

Newton's third law expressed in English language: The force exerted by particle A on B equals that the force exerted by particle B on A in magnitude but opposite in direction.

Newton's third law stated in L.O.M. :

enter image description here

Notice that the SAME truth about the physical world was expressed in two different ways in two different languages: English and L.O.M..

Okay, enough of examples that show that L.O.M. is a language and let's give examples of things that are mathematics but not a part of L.O.M.. These are the mathematical truths. Just like how a physics truth (that of Newton's third) law was expressed in two different languages above, I will also state a mathematics truth (Fermat's little theorem) in two different languages:

Statement of the Euler's theorem in English language: For any number p which is not divisible by two and has exactly two divisors, it must be the case that subtracting one from two raised to the power of p-1 yields an answer that is divisible by p.

Statement of Euler's theorem in the language L.O.M.:

enter image description here

When a reasonable person sees a claim like this, he or she can't help but wonder why should 2^(p-1)-1 be divisible by p for any odd prime, and that's not a matter of language. Languages to a large extent can be chosen arbitrarily that's why different cultures develop different languages but they do not develop different mathematical truths or different physics truths. Another example of a truth about high school level mathematics is the Taylor expansion of the sine function:

enter image description here

The left hand side of the above equation expresses the ratio between the hypotenuse and the opposite side of a certain right angled triangle, while the right hand side has an infinite sum of powers of $x^k$ divided by the number of ways to permute $k$ objects. A reasonable person can't help but wonder why the hell is something geometric like the sine of an angle getting related to polynomials divided by a combinatorial cofficent like k!. You might answer its because of Taylor's theorem, but what makes Taylor's theorem true ? It certainly isn't just a linguistic convention like denoting blue by bleu in french, it's not a human choice. !! It's a mathematical truth and it has an explanation worthy of being understood!! Different human civilizations develop different languages but they don't develop different Taylor expansions of the sine function :D The central limit theorem is another example of a mathematical truth. It could be stated in lots of languages, but the truth is the same. I only mentioned examples of highschool mathematics or early undergraduate mathematics, but the totality of known mathematical truths goes really deep. See the classification of finite simple groups for instance.

Hopefully, I gave lots of examples to illustrate the difference between mathematics and L.O.M. If you are still not convinced, consider this silly question:

Since any physics textbook consists of math symbols and english words, why is physics not just a language made out of a mix of mathematical symbols and english words ?

You would probably answer that physics is about the totality of truths about our universe, and these truths are getting expressed in english or/and math symbols. In a similar way, mathematics is about the truths about mathematical objects (shapes, numbers, algebra,...) and these truths can be expressed in english and /or mathematical symbols (L.O.M.)

Math also doesn't exclusively describe anything. There are always other representations (logic, computation, natural language, pictures) for any mathematical formulation.

As I mentioned above, thinking of math as descriptive tool is wrong. By the way, formal logic and computation are parts of mathematics. Formal logic could is studied in the area of mathematics called mathematical logic and computation is really the study of various questions about the mathematical objects called Turing machines, so arguably theoretical computer science (in particular something like computational complexity theory and computability theory) are just mathematics. The thing is that due to Godel's completness theorem, any (almost all ?) formal system could be studied within mathematics. Computation and formal logic are formal systems so they automatically become mathematics.

Amr
  • 417
  • 4
  • 13
  • Comments are not for extended discussion; this conversation has been [moved to chat](https://chat.stackexchange.com/rooms/132063/discussion-on-answer-by-amr-why-dont-we-say-the-unreasonable-effectiveness-of). – Philip Klöcking Dec 05 '21 at 09:35
0

Natural language is ad hoc and evolutionary, that it is effective is not surprising given that people can create or modify natural language in any way that they see fit. Where it works well, it's a case of the water fitting the puddle.

In the estimation of some people, math is not arbitrary in this way; mathematics is a particular, unitary, logical structure where no part can be altered without destroying the whole. If it were the case that there is this kind of singleton logical structure, one that exists but not as a physical entity, then it is somewhat curious that this particular abstract thing should, apparently, map so directly onto the completely different domain of physical existence.

In some respects, this is just a long-winded way of saying that I suspect that the people endorsing the "unreasonable effectiveness of mathematics" tend to overlap with mathematical realists -- and there just aren't many "linguistic realists" that take the same kind of metaphysical view of language.

Dave
  • 5,261
  • 1
  • 18
  • 51