The "true" circle of fifths is not a circle at all, but more of a spiral. A fifth above an A# is not an F, it's an E# (an F would be a diminished 6th). Another fifth (up from E#) is not C, but B# (for the same reason as before). This, therefore, leads us to the following: C->G->D->A->E->B->F#->C#->G#->D#->A#->E#->B#->F##->C##->G##->D##->A##->E##->B##->F###->C### ad infinitum). To avoid diagramming an infinite spiral (in both directions), we went ahead and allowed a couple diminished 6ths to help connect up the ends and bring us full circle (#nailedit).
So why, then, do we have the enharmonic keys at the bottom at all? Couldn't we have just picked one or the other and moved our connecting diminished 6th accordingly? We are, after all, already completely ignoring Fb and showing only E, so why not ignore Cb, Gb and C# as well?
Let's think of it in a slightly different way. Instead of the letter name of the root, consider the number of sharps or flats in the key. Since we only have 7 notes to choose from, it makes sense (for completeness) to start with everything flat (Cb), remove one flat at a time until we get to C, then add one sharp at a time until everything is sharp (C#). Then we combine the enharmonic overlaps and we're left with the circle of fifths as we know it.
In the end, the circle of fifths is a reference tool, not a definition. Do you have to draw it symmetrically? No, you can draw it however you want. Is it a good idea? Yes, I think so. Does it completely and utterly drive me crazy if there is one flat unaccounted for and it's not perfectly symmetric? Absolutely! ;)
(One other interesting way to think about it is by the leading tone, or the major 7th above (and half step below) the root. All other chords in a major key are shared between several keys, but the diminished chord on the 7th degree is unique to its respective key. This is why it wants to resolve to the root chord so badly (it's all its got!). By finding the root for every leading tone we get the following: B -> C major, B#/C -> C#/Db major, C# -> D major, D -> Eb major, D# -> E major, E -> F major, E#/F -> F#/Gb major, F# -> G major, G -> Ab major, G# -> A major, A -> Bb major, A# -> B major and Bb -> Cb major. This gives us every key on the circle of fifths (in a different order of course), including Cb. Without Cb, the Bb leading tone has no key to resolve to )
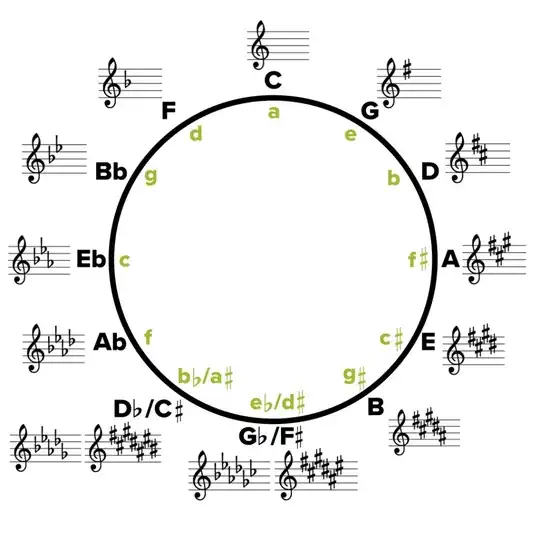 So why have B major and Cb major be different keys? Why does the circle of fifths have to have this symmetry to it?
So why have B major and Cb major be different keys? Why does the circle of fifths have to have this symmetry to it?